题目内容
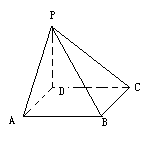
如图,四棱锥P—ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC=![]() a,且PD是四棱锥的高。
a,且PD是四棱锥的高。
(1)在这个四棱锥中放入一个球,求球的最大半径。
(2)求四棱锥外接球的半径。
证明:(1)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连结SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R。
VP——ABCD=![]() ·S
·S![]() ABCD·PD=
ABCD·PD=![]() ·a·a·a
·a·a·a
=![]() a3,S
a3,S![]() PAD= S
PAD= S![]() PDC=
PDC=![]() ·a·a=
·a·a=![]() a2,
a2,
S![]() PAB= S
PAB= S![]() PBC=
PBC=![]() ·a·
·a·![]() a=
a=![]() a2
a2
S![]() ABCD=a2。
ABCD=a2。
VP—ABCD= VS—PDA+ VS——PDC+ VS-ABCD+ VS—PAB+ VS—PBC,
![]() a3=
a3=![]() R(S
R(S![]() PAD+ S
PAD+ S![]() PDC+ S
PDC+ S![]() PAB+ S
PAB+ S![]() PBC+ S
PBC+ S![]() ABCD),
ABCD),
![]() a3=
a3=![]() R(
R(![]() a2+
a2+![]() a2+
a2+![]() a2+
a2+
![]() a2+a2),
a2+a2),
![]() R(2+
R(2+![]() )a2=
)a2=![]() a3,
a3,
∴R=![]() =
=![]() a=(1-
a=(1-![]() )a
)a
∴球的最大半径为(1-![]() )a
)a
(2)设PB的中点为F,
∵ 在Rt![]() PDB中,FP=FB=FD,
PDB中,FP=FB=FD,
在Rt![]() PAB中,FA=FP=FB,
PAB中,FA=FP=FB,
在Rt![]() PBC中,FP=FB=FC,
PBC中,FP=FB=FC,
∴FP=FB=FA=FC=FD。
∴F为四棱锥外接球的球心。
则FP为外接球的半径
∵FB=![]() PB,∴FB=
PB,∴FB=![]() a。
a。
∴四棱锥的外接球的半径为![]() a。
a。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=