题目内容
已知“一个圆和一个正方形的周长相等时,圆的面积比正方形的面积大”.(1)设一个圆和一个正方形的周长相等,都为l,请你用l分别表示出圆和正方形的面积,并用分析法证明该命题;
(2)类比球体与正方体,写出一个正确的命题(不要求证明).
分析:(1)依题意,圆的面积为π•(
)2,正方形的面积为(
)2,根据分析法的证明步骤可得结论;
(2)周长类比表面积,面积类比体积,即可得出结论.
| l |
| 2π |
| l |
| 4 |
(2)周长类比表面积,面积类比体积,即可得出结论.
解答:解:(1)依题意,圆的面积为π•(
)2,正方形的面积为(
)2.
因此本题只需证明π•(
)2>(
)2.
要证明上式,只需证明
>
,
两边同乘以正数
,得
>
.
因此,只需证明4>π.
因为4>π恒成立,所以π•(
)2>(
)2.
这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积大.
(2)一个球与一个正方体的表面积相等时,球的体积比正方体的体积大.
| l |
| 2π |
| l |
| 4 |
因此本题只需证明π•(
| l |
| 2π |
| l |
| 4 |
要证明上式,只需证明
| πl2 |
| 4π2 |
| l2 |
| 16 |
两边同乘以正数
| 4 |
| l2 |
| 1 |
| π |
| 1 |
| 4 |
因此,只需证明4>π.
因为4>π恒成立,所以π•(
| l |
| 2π |
| l |
| 4 |
这就证明了如果一个圆和一个正方形的周长相等,那么圆的面积比正方形的面积大.
(2)一个球与一个正方体的表面积相等时,球的体积比正方体的体积大.
点评:本题考查类比方法的运用,考查分析法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 ,称圆心在原点O、半径是
,称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为 ,其短轴的一个端点到点
,其短轴的一个端点到点 的距离为
的距离为 .
. 是椭圆C的“准圆”与
是椭圆C的“准圆”与 轴正半轴的交点,
轴正半轴的交点, 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且 轴,求
轴,求 的取值范围;
的取值范围; ,过点
,过点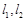 ,使得
,使得