题目内容
已知函数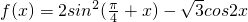 ,
,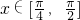 .
.
(1)求f(x)的最大值和最小值;
(2)求f(x)的单调区间.
解:(1)由题意,函数可化为:
∵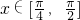
∴
∴
∴f(x)∈[2,3]
∴f(x)的最大值和最小值分别为3,2;
(2)∵
∴ 时,函数单调增,
时,函数单调增, 时,函数单调减.
时,函数单调减.
∴函数单调增区间为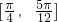 ,函数单调减区间为
,函数单调减区间为
分析:(1)先利用二倍角公式化简,再利用差角的正弦函数化简函数,可得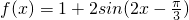 ,根据已知角的范围,确定
,根据已知角的范围,确定 ,从而得解;
,从而得解;
(2)根据) ,可得
,可得 时,函数单调增,
时,函数单调增, 时,函数单调减,故可解.
时,函数单调减,故可解.
点评:本题以三角函数为载体,考查三角函数的最值,考查函数的单调性,关键是对函数的化简.

∵
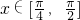
∴

∴

∴f(x)∈[2,3]
∴f(x)的最大值和最小值分别为3,2;
(2)∵

∴
 时,函数单调增,
时,函数单调增, 时,函数单调减.
时,函数单调减.∴函数单调增区间为
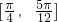 ,函数单调减区间为
,函数单调减区间为
分析:(1)先利用二倍角公式化简,再利用差角的正弦函数化简函数,可得
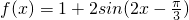 ,根据已知角的范围,确定
,根据已知角的范围,确定 ,从而得解;
,从而得解;(2)根据)
 ,可得
,可得 时,函数单调增,
时,函数单调增, 时,函数单调减,故可解.
时,函数单调减,故可解.点评:本题以三角函数为载体,考查三角函数的最值,考查函数的单调性,关键是对函数的化简.

练习册系列答案
相关题目