题目内容
9.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a-c=$\frac{\sqrt{6}}{6}$b,sinB=$\sqrt{6}$sinC.(Ⅰ)求cosA的值;
(Ⅱ)求cos(2A-$\frac{π}{3}$)的值.
分析 (Ⅰ)由正弦定理解余弦定理即可求cosA的值;
(Ⅱ)利用二倍角的正弦、余弦公式求得sin2A、cos2A,在利用两角差的余弦公式求得$cos(2A-\frac{π}{3})$.
解答 解:(Ⅰ)在△ABC中,由$\frac{b}{sinB}=\frac{c}{sinC}$及$sinB=\sqrt{6}sinC$,
可得$b=\sqrt{6}c$,(2分)
又由$a-c=\frac{{\sqrt{6}}}{6}b$,有a=2c(4分)
所以cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{6{c}^{2}+{c}^{2}-4{c}^{2}}{2\sqrt{6}{c}^{2}}$=$\frac{\sqrt{6}}{4}$; (6分)
(Ⅱ)在△ABC中,由$cosA=\frac{{\sqrt{6}}}{4}$,可得$sinA=\frac{{\sqrt{10}}}{4}$,(7分)
所以$cos2A=2{cos^2}A-1=-\frac{1}{4},sin2A=2sinAcosA=\frac{{\sqrt{15}}}{4}$,(9分)
所以cos(2A-$\frac{π}{3}$)=cos2Acos$\frac{π}{3}$+sin2Asin$\frac{π}{3}$=$-\frac{1}{4}×\frac{1}{2}$+$\frac{\sqrt{15}}{4}$×$\frac{\sqrt{3}}{2}$=$\frac{-1+3\sqrt{5}}{8}$.(12分)
点评 本题主要考查解三角形的应用,在求解三角形时,要注意正弦定理、余弦定理的正确使用,在求解两角和与差的三角函数时,要注意结合角的范围,求出要用到的角的三角函数值,并利用公式正确求解.

 名校课堂系列答案
名校课堂系列答案| A. | [-1,1] | B. | [-$\frac{1}{2},\frac{1}{2}$] | C. | [-$\sqrt{2},\sqrt{2}$] | D. | [-$\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$] |
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
文化程度与月收入列联表(单位:人)
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A. | 1% | B. | 99% | C. | 2.5% | D. | 97.5% |
| A. | $\frac{2}{3}$或$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
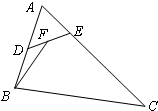 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )