题目内容
已知椭圆C: (a>b>0)的一个焦点为F(1,0),点(-1,
(a>b>0)的一个焦点为F(1,0),点(-1, )在椭圆C上,点T满足
)在椭圆C上,点T满足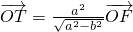 (其中O为坐标原点),过点F作一直线交椭圆于P、Q两点.
(其中O为坐标原点),过点F作一直线交椭圆于P、Q两点.
(1)求椭圆C的方程;
(2)求△PQT面积的最大值;
(3)设点P′为点P关于x轴的对称点,判断 与
与 的位置关系,并说明理由.
的位置关系,并说明理由.
(理)解:(1)∵椭圆C: (a>b>0)的一个焦点为F(1,0),点(-1,
(a>b>0)的一个焦点为F(1,0),点(-1, )在椭圆C上,
)在椭圆C上,
∴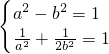 ,
,
解得a2=2,b2=1,
所以,椭圆方程为 .
.
(2)由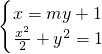 ,得(m2+2)y2+2my-1=0,
,得(m2+2)y2+2my-1=0,
设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).
S△PQT= |FT||y1-y2|=
|FT||y1-y2|= •
•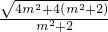 =
=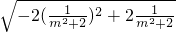 ,
,
令t=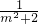 ,则t∈(0,
,则t∈(0, ],
],
则S△PQT=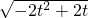 =
=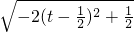 ≤
≤ ,
,
当且仅当t= ,即m=0(此时PQ垂直于x轴)时等号成立,
,即m=0(此时PQ垂直于x轴)时等号成立,
所以S△PQT的最大值是 .
.
(3) 与
与 共线
共线
P′(x1,-y1),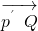 =(x2-x1,y2+y1),
=(x2-x1,y2+y1),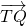 =(x2-2,y2),
=(x2-2,y2),
由(x2-x1)y2-(x2-2)(y1+y2)
=-x1y2-x2y1+2(y1+y2)
=-(my1+1)y2-(my2+1)y1+2(y1+y2)
=-2my1y2+(y1+y2)
=-2m• +
+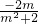 =0,
=0,
所以,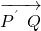 与
与 共线
共线
分析:(1)由椭圆C: (a>b>0)的一个焦点为F(1,0),点(-1,
(a>b>0)的一个焦点为F(1,0),点(-1, )在椭圆C上,知
)在椭圆C上,知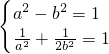 ,由此能求出椭圆方程.
,由此能求出椭圆方程.
(2)由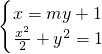 ,得(m2+2)y2+2my-1=0,设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).S△PQT=
,得(m2+2)y2+2my-1=0,设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).S△PQT= |FT||y1-y2|,由此能推导出S△PQT的最大值.
|FT||y1-y2|,由此能推导出S△PQT的最大值.
(3) 与
与 共线,P′(x1,-y1),
共线,P′(x1,-y1),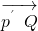 =(x2-x1,y2+y1),
=(x2-x1,y2+y1),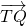 =(x2-2,y2),由(x2-x1)y2-(x2-2)(y1+y2)=0,得到
=(x2-2,y2),由(x2-x1)y2-(x2-2)(y1+y2)=0,得到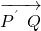 与
与 共线.
共线.
点评:本题考查椭圆方程的求法,考查三角形面积最大值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
 (a>b>0)的一个焦点为F(1,0),点(-1,
(a>b>0)的一个焦点为F(1,0),点(-1, )在椭圆C上,
)在椭圆C上,∴
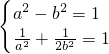 ,
,解得a2=2,b2=1,
所以,椭圆方程为
 .
.(2)由
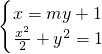 ,得(m2+2)y2+2my-1=0,
,得(m2+2)y2+2my-1=0,设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).
S△PQT=
 |FT||y1-y2|=
|FT||y1-y2|= •
•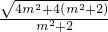 =
=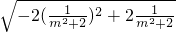 ,
,令t=
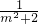 ,则t∈(0,
,则t∈(0, ],
],则S△PQT=
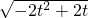 =
=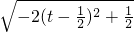 ≤
≤ ,
,当且仅当t=
 ,即m=0(此时PQ垂直于x轴)时等号成立,
,即m=0(此时PQ垂直于x轴)时等号成立,所以S△PQT的最大值是
 .
.(3)
 与
与 共线
共线 P′(x1,-y1),
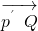 =(x2-x1,y2+y1),
=(x2-x1,y2+y1),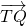 =(x2-2,y2),
=(x2-2,y2),由(x2-x1)y2-(x2-2)(y1+y2)
=-x1y2-x2y1+2(y1+y2)
=-(my1+1)y2-(my2+1)y1+2(y1+y2)
=-2my1y2+(y1+y2)
=-2m•
 +
+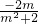 =0,
=0,所以,
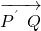 与
与 共线
共线分析:(1)由椭圆C:
 (a>b>0)的一个焦点为F(1,0),点(-1,
(a>b>0)的一个焦点为F(1,0),点(-1, )在椭圆C上,知
)在椭圆C上,知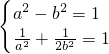 ,由此能求出椭圆方程.
,由此能求出椭圆方程.(2)由
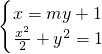 ,得(m2+2)y2+2my-1=0,设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).S△PQT=
,得(m2+2)y2+2my-1=0,设P(x1,y1),Q(x2,y2),由条件可知,点T(2,0).S△PQT= |FT||y1-y2|,由此能推导出S△PQT的最大值.
|FT||y1-y2|,由此能推导出S△PQT的最大值.(3)
 与
与 共线,P′(x1,-y1),
共线,P′(x1,-y1),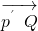 =(x2-x1,y2+y1),
=(x2-x1,y2+y1),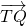 =(x2-2,y2),由(x2-x1)y2-(x2-2)(y1+y2)=0,得到
=(x2-2,y2),由(x2-x1)y2-(x2-2)(y1+y2)=0,得到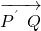 与
与 共线.
共线.点评:本题考查椭圆方程的求法,考查三角形面积最大值的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
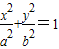 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
. (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;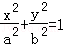 (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 .
. ,求点Q的轨迹方程.
,求点Q的轨迹方程. (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N. 时,求k的值.
时,求k的值. +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若 。则
。则 ( )
( )  (D)
(D)