题目内容
若函数y=f(x)满足f'(x)>f(x),则当a>0时,f(a)与eaf(0)的大小关系为
- A.f(a)<eaf(0)
- B.f(a)>eaf(0)
- C.f(a)=eaf(0)
- D.与f(x)或a的值有关,不能确定
B
分析:结合选项,构造函数g(x)=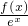 ,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得所证不等式
,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得所证不等式
解答:设g(x)=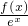 ,
,
∵f'(x)>f(x),
∴g′(x)= >0
>0
∴函数g(x)为R上的增函数
∵a>0
∴g(a)>g(0)
即
∴f(a)>eaf(0)
故选 B
点评:本题考查了利用函数单调性比较大小的方法,恰当的构造函数,并能利用导数研究其性质是解决本题的关键
分析:结合选项,构造函数g(x)=
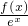 ,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得所证不等式
,利用导数研究其单调性,注意到已知f'(x)>f(x),可得g(x)为单调增函数,最后由a>0,代入函数解析式即可得所证不等式解答:设g(x)=
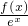 ,
,∵f'(x)>f(x),
∴g′(x)=
 >0
>0∴函数g(x)为R上的增函数
∵a>0
∴g(a)>g(0)
即

∴f(a)>eaf(0)
故选 B
点评:本题考查了利用函数单调性比较大小的方法,恰当的构造函数,并能利用导数研究其性质是解决本题的关键

练习册系列答案
相关题目