题目内容
在复平面中,已知A,B,C三点分别对应复数2+i,4+3i,3+5i,又知点D与这三点构成平行四边形,求点D对应的复数.
分析:该题应考虑三种情形,然后根据平行四边形对角线上两顶点的和相等建立等式,可求出点D对应的复数.
解答:解:由于平行四边形对角线互相平分
故在复平面上,若平行四边形ABCD,则四个顶点满足:
A、C两顶点的和等于C、D两个顶点的和
即:2+i+3+5i=4+3i+Z
故Z=1+3i
若平行四边形ABDC,则四个顶点满足:
A、D两顶点的和等于B、C两个顶点的和
即:2+i+Z=4+3i+3+5i
故Z=5+7i
若平行四边形ADBC,则四个顶点满足:
A、B两顶点的和等于D、C两个顶点的和
即:2+i+4+3i=Z+3+5i
故Z=3-i
点D对应的复数为3-i或1+3i或5+7i
故在复平面上,若平行四边形ABCD,则四个顶点满足:
A、C两顶点的和等于C、D两个顶点的和
即:2+i+3+5i=4+3i+Z
故Z=1+3i
若平行四边形ABDC,则四个顶点满足:
A、D两顶点的和等于B、C两个顶点的和
即:2+i+Z=4+3i+3+5i
故Z=5+7i
若平行四边形ADBC,则四个顶点满足:
A、B两顶点的和等于D、C两个顶点的和
即:2+i+4+3i=Z+3+5i
故Z=3-i
点D对应的复数为3-i或1+3i或5+7i
点评:本题主要考查了复数代数形式的加减运算,以及复数的几何意义,同时考查了分类讨论的思想,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 ③
③ ④
④ .
.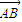 +
+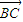 =
=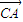 ;
;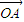 +
+ =
=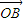 ;
;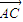 =
=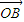 -2
-2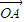 .
.