题目内容
设椭圆 的离心率为
的离心率为 ,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)
,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)
- A.必在圆x2+y2=2内
- B.必在圆x2+y2=2上
- C.必在圆x2+y2=2外
- D.以上三种情形都有可能
A
分析:由题意可求得c= a,b=
a,b= a,从而可求得x1和x2,利用韦达定理可求得
a,从而可求得x1和x2,利用韦达定理可求得 +
+ 的值,从而可判断点P与圆x2+y2=2的关系.
的值,从而可判断点P与圆x2+y2=2的关系.
解答:∵椭圆的离心率e= =
= ,
,
∴c= a,b=
a,b=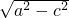 =
= a,
a,
∴ax2+bx-c=ax2+ ax-
ax- a=0,
a=0,
∵a≠0,
∴x2+ x-
x- =0,又该方程两个实根分别为x1和x2,
=0,又该方程两个实根分别为x1和x2,
∴x1+x2=- ,x1x2=-
,x1x2=- ,
,
∴ +
+ =
=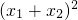 -2x1x2=
-2x1x2= +1<2.
+1<2.
∴点P在圆x2+y2=2的内部.
故选A.
点评:本题考查椭圆的简单性质,考查点与圆的位置关系,求得c,b与a的关系是关键,属于中档题.
分析:由题意可求得c=
 a,b=
a,b= a,从而可求得x1和x2,利用韦达定理可求得
a,从而可求得x1和x2,利用韦达定理可求得 +
+ 的值,从而可判断点P与圆x2+y2=2的关系.
的值,从而可判断点P与圆x2+y2=2的关系.解答:∵椭圆的离心率e=
 =
= ,
,∴c=
 a,b=
a,b=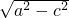 =
= a,
a,∴ax2+bx-c=ax2+
 ax-
ax- a=0,
a=0,∵a≠0,
∴x2+
 x-
x- =0,又该方程两个实根分别为x1和x2,
=0,又该方程两个实根分别为x1和x2,∴x1+x2=-
 ,x1x2=-
,x1x2=- ,
,∴
 +
+ =
=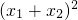 -2x1x2=
-2x1x2= +1<2.
+1<2.∴点P在圆x2+y2=2的内部.
故选A.
点评:本题考查椭圆的简单性质,考查点与圆的位置关系,求得c,b与a的关系是关键,属于中档题.

练习册系列答案
相关题目
 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( ) 内
B.必在圆
内
B.必在圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( ) 内 B.必在圆
内 B.必在圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 (
)
(
) 内
B.必在圆
内
B.必在圆 的离心率为
的离心率为 ,右焦点为
,右焦点为 ,方程
,方程 的两个实根分别为
的两个实根分别为 和
和 ,则点
,则点 ( )
( ) 内 B.必在圆
内 B.必在圆