题目内容
函数f（x）=2x2-kx+3在[2，+∞）上是增函数，则k的取值范围是________．
（-∞，8]
分析：根据二次函数的性质可得，f（x）=2x2-kx+3的单调增区间为：[
），结合已知函数f（x）=2x2-kx+3在[2，+∞]上是增函数可得
，从而可求k的取值范围
解答：∵f（x）=2x2-kx+3的对称轴为：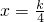
∴函数的单调增区间为：[）
又∵函数f（x）=2x2-kx+3在[2，+∞]上是增函数
∴
∴
解可得，k≤8
故答案为：（-∞，8]．
点评：本题主要考查了二次函数的单调性的应用，判定二次函数的单调区间的关键是要确定函数的对称轴，另外，解答本题时要注意函数在区间I上单调递增与函数的单调增区间为I的区别
分析：根据二次函数的性质可得，f（x）=2x2-kx+3的单调增区间为：[
），结合已知函数f（x）=2x2-kx+3在[2，+∞]上是增函数可得，从而可求k的取值范围解答：∵f（x）=2x2-kx+3的对称轴为：
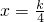
∴函数的单调增区间为：[
）又∵函数f（x）=2x2-kx+3在[2，+∞]上是增函数
∴
∴
解可得，k≤8故答案为：（-∞，8]．
点评：本题主要考查了二次函数的单调性的应用，判定二次函数的单调区间的关键是要确定函数的对称轴，另外，解答本题时要注意函数在区间I上单调递增与函数的单调增区间为I的区别
练习册系列答案
相关题目
函数f（x）=2x2-6x+1在区间[-1，1]上的最小值为（ ）
| A、9 | ||
| B、-3 | ||
C、
| ||
D、
|