题目内容
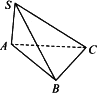
如图，
S为△ABC所在平面外一点．SA=SB=SC，且∠ASC=90°，∠ASB=∠BSC=60°，求证：平面ASC⊥平面ABC．
答案：略
解析：
解析：
|
证明 设 SA=a，则SB=SC=a．∵∠ ASC=90°，∠ASB=∠BSC=60°，∴ ，AB=BC=a，
则  ，∴∠ABC=90°．
如图，取 AC中点O，连SO，BO．则 SO⊥AC，BO⊥AC，∠SOB为二面角S－AC－B的平面角．∵  ， ，
∴∠ SOB=90°，∴平面ASC⊥平面ABC．
|
练习册系列答案
相关题目
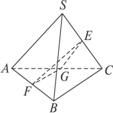
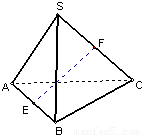
如图，S是边长为a的正三角ABC所在平面外一点，SA=SB=SC=a，E、F是AB和SC的中点，则异面直线SA与EF所成的角为
