题目内容
函数f(x)=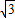 cos2x-sin2x的单调减区间为( )
cos2x-sin2x的单调减区间为( )A.[kπ+
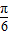 ,π+
,π+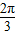 ],k∈Z
],k∈ZB.[kπ-
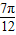 ,π-
,π-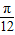 ],k∈Z
],k∈ZC.[2kπ-
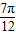 ,2kπ-
,2kπ-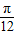 ],k∈Z
],k∈ZD.[kπ-
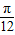 ,kπ+
,kπ+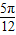 ],k∈Z
],k∈Z
【答案】分析:化简可得函数f(x)=-2sin(2x-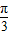 ),本题即求y=2sin(2x-
),本题即求y=2sin(2x-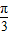 )的增区间.由 2kπ-
)的增区间.由 2kπ-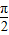 ≤2x-
≤2x-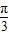 ≤2kπ+
≤2kπ+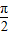 ,k∈z,求得x的范围,即得所求.
,k∈z,求得x的范围,即得所求.
解答:解:∵函数f(x)=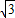 cos2x-sin2x=2(
cos2x-sin2x=2(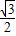 cos2x-
cos2x- sin2x)=2sin(
sin2x)=2sin(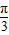 -2x)=-2sin(2x-
-2x)=-2sin(2x-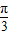 ),
),
故本题即求y=2sin(2x-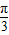 )的增区间.
)的增区间.
由 2kπ-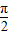 ≤2x-
≤2x-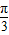 ≤2kπ+
≤2kπ+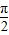 ,k∈z,可得 kπ-
,k∈z,可得 kπ-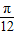 ≤x≤2kπ≤kπ+
≤x≤2kπ≤kπ+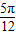 ,k∈z.
,k∈z.
故y=2sin(2x-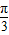 )的增区间为[kπ-
)的增区间为[kπ-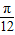 ,kπ+
,kπ+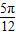 ],k∈Z,
],k∈Z,
故选D.
点评:本题主要考查两角和差的正弦公式,正弦函数的单调增区间的求法,体现了等价转化的数学思想,属于中档题.
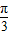 ),本题即求y=2sin(2x-
),本题即求y=2sin(2x-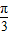 )的增区间.由 2kπ-
)的增区间.由 2kπ-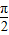 ≤2x-
≤2x-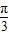 ≤2kπ+
≤2kπ+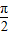 ,k∈z,求得x的范围,即得所求.
,k∈z,求得x的范围,即得所求.解答:解:∵函数f(x)=
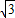 cos2x-sin2x=2(
cos2x-sin2x=2(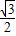 cos2x-
cos2x- sin2x)=2sin(
sin2x)=2sin(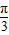 -2x)=-2sin(2x-
-2x)=-2sin(2x-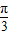 ),
),故本题即求y=2sin(2x-
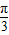 )的增区间.
)的增区间.由 2kπ-
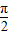 ≤2x-
≤2x-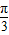 ≤2kπ+
≤2kπ+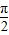 ,k∈z,可得 kπ-
,k∈z,可得 kπ-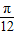 ≤x≤2kπ≤kπ+
≤x≤2kπ≤kπ+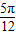 ,k∈z.
,k∈z.故y=2sin(2x-
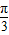 )的增区间为[kπ-
)的增区间为[kπ-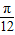 ,kπ+
,kπ+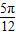 ],k∈Z,
],k∈Z,故选D.
点评:本题主要考查两角和差的正弦公式,正弦函数的单调增区间的求法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目