题目内容
已知函数f(x)=alog2x+blog3x+2,且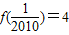 ,则f(2010)的值为( )
,则f(2010)的值为( )A.-4
B.2
C.-2
D.0
【答案】分析:利用对数的运算性质,可得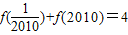 ,因此f(2010)=4-
,因此f(2010)=4-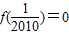 ,即f(2010)的值为零.
,即f(2010)的值为零.
解答:解:由函数f(x)=alog2x+blog3x+2,
得f(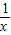 )=alog2
)=alog2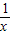 +blog3
+blog3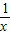 +2=-alog2x-blog3x+2=4-(alog2x+blog3x+2),
+2=-alog2x-blog3x+2=4-(alog2x+blog3x+2),
因此f(x)+f(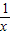 )=4
)=4
再令x=2010得f(2010)+f(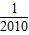 )=4
)=4
所以f(2010)=4-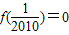 ,
,
故选D
点评:本题考查了对数的运算性质,和函数的简单性质,属于基础题.利用互为倒数的两个自变量的函数值之间的关系,是解决本题的关键.
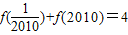 ,因此f(2010)=4-
,因此f(2010)=4-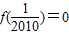 ,即f(2010)的值为零.
,即f(2010)的值为零.解答:解:由函数f(x)=alog2x+blog3x+2,
得f(
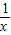 )=alog2
)=alog2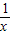 +blog3
+blog3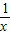 +2=-alog2x-blog3x+2=4-(alog2x+blog3x+2),
+2=-alog2x-blog3x+2=4-(alog2x+blog3x+2),因此f(x)+f(
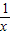 )=4
)=4再令x=2010得f(2010)+f(
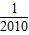 )=4
)=4所以f(2010)=4-
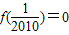 ,
,故选D
点评:本题考查了对数的运算性质,和函数的简单性质,属于基础题.利用互为倒数的两个自变量的函数值之间的关系,是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目