题目内容
已知![]() 为二次函数,不等式
为二次函数,不等式![]() 的解集为
的解集为![]() ,且对任意
,且对任意![]() ,
,![]() 恒有
恒有![]() ,
,![]() .数列
.数列![]() 满足
满足![]() ,
,![]()
(1)求函数![]() 的解析式;(2)设
的解析式;(2)设![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(3)若(2)中数列![]() 的前
的前![]() 项和为
项和为![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
解:(1)依题意,![]()
![]() ,
,
即![]() ..........................2分
..........................2分
令![]() ,则
,则![]() ,有
,有![]() ,
,
得![]() ,即
,即![]() ,得
,得![]() .
.![]() . ....................5分
. ....................5分
(2)![]() ,则
,则![]() ..........................7分
..........................7分
即![]() ,两边取倒数,得
,两边取倒数,得![]() ,即
,即![]() .
.
![]() 数列
数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列.
的等差数列.
![]() . .......................... 10分
. .......................... 10分
(3)![]()
![]()
![]() . ..........................12分
. ..........................12分
①当![]() 为偶数时
为偶数时
![]()
 ..........................14分
..........................14分
②当![]() 为奇数时
为奇数时
![]()
![]()
综上, ..........................16分
..........................16分

练习册系列答案
相关题目
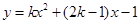 与x轴交点的横坐标为
与x轴交点的横坐标为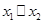 (
( ).则对于下列结论:①当
).则对于下列结论:①当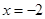 时,
时,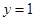 ;②当
;②当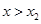 时,
时,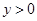 ;③关于x方程
;③关于x方程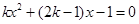 有两个不等实根;④
有两个不等实根;④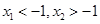 ;⑤
;⑤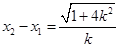 .其中正确的结论是 .(只需填序号)
.其中正确的结论是 .(只需填序号)