题目内容
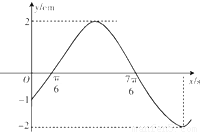
 如图是某筒谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某筒谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
(1)根据图象求函数y=f(x)的解析式;
(2)若函数g(x)=f(x+
| π |
| 6 |
| ∫ | π a |
分析:(1)由图象可求得A=2,ω=1,从而可得函数的解析式;
(2)由(1)知g(x)=f(x+
)=2sinx,利用积分公式可求得
g(x)dx=
2sinxdx=-2cosx
=-2cosπ+2cosa=3,继而可求得a的值.
(2)由(1)知g(x)=f(x+
| π |
| 6 |
| ∫ | π a |
| ∫ | π a |
| | | π a |
解答:解:(1)∵A>0,f(x)=Asin(ωx+φ)(x≥0)知
f(x)max=A=2,f(x)min=-A=-2,
∴A=2…2′
由
T=
-
=π,
∴T=2π,又T=
(ω>0)
∴
=2π,
∴ω=1…4′
∴函数的解析式为y=f(x)=2sin(x+φ),
由图可知,
+φ=2kπ,(也可用
+φ=π来解).
∴φ=-
.
∴所求的函数的解析式为y=f(x)=2sin(x-
)…6′
(2)由(1)知g(x)=f(x+
)=2sinx.
∵
g(x)dx=
2sinxdx=-2cosx
=-2cosπ+2cosa=3,
∴cosa=
,又0<a<π,
∴a=
…12′
f(x)max=A=2,f(x)min=-A=-2,
∴A=2…2′
由
| 1 |
| 2 |
| 7π |
| 6 |
| π |
| 6 |
∴T=2π,又T=
| 2π |
| ω |
∴
| 2π |
| ω |
∴ω=1…4′
∴函数的解析式为y=f(x)=2sin(x+φ),
由图可知,
| π |
| 6 |
| 7π |
| 6 |
∴φ=-
| π |
| 6 |
∴所求的函数的解析式为y=f(x)=2sin(x-
| π |
| 6 |
(2)由(1)知g(x)=f(x+
| π |
| 6 |
∵
| ∫ | π a |
| ∫ | π a |
| | | π a |
∴cosa=
| 1 |
| 2 |
∴a=
| π |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式及定积分的简单应用,关键在于数量掌握求A,ω的方法及定积分公式,属于中档题.

练习册系列答案
相关题目
 如图是某筒谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,-
如图是某筒谐运动的一段图象,其函数模型是f(x)=Asin(ωx+φ)(x≥0),其中A>0,ω>0,- <φ<
<φ< ).实数a满足0<a<π.且
).实数a满足0<a<π.且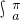 g(x)dx=3.求a的值.
g(x)dx=3.求a的值. <φ<
<φ< .
. ).实数a满足0<a<π.且
).实数a满足0<a<π.且 g(x)dx=3.求a的值.
g(x)dx=3.求a的值.