题目内容
已知关于n的不等式2n2-n-3<(5-λ)(n+1)2n对任意n∈N*恒成立,则实数λ的取值范围是________.
λ<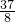
分析:根据不等式的基本性质,将原不等式转化为:5-λ>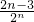 对任意n∈N*恒成立,通过研究右边式子的单调性,可得当n=3时,右边的最大值为
对任意n∈N*恒成立,通过研究右边式子的单调性,可得当n=3时,右边的最大值为 ,从而5-λ>
,从而5-λ> ,解之即得λ的取值范围.
,解之即得λ的取值范围.
解答:∵n∈N*,∴n+1>0
在不等式2n2-n-3<(5-λ)(n+1)2n两边都除以n+1,得
2n-3<(5-λ)2n对任意n∈N*恒成立,即5-λ>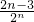
设f(n)=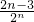 ,可得
,可得
当n=1时,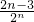 =-
=- <0
<0
当n≥2时,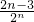 >0,
>0, =
= •
• =
=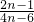
可得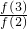 =
= >1,
>1,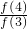 =
= <1,
<1,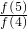 =
= <1,…
<1,…
由此可得,f(2)<f(3),f(3)>f(4),f(4)>f(5),…
∴f(n)的最大值为f(3)= ,
,
要使原不等式对任意n∈N*恒成立,必须5-λ> ,解之得λ<
,解之得λ<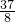
故答案为:λ<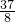
点评:本题给出关于n的式子恒成立,求参数λ的取值范围,着重考查了不等式的基本性质、不等式恒成立和简单的演绎推理等知识,属于中档题.
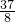
分析:根据不等式的基本性质,将原不等式转化为:5-λ>
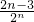 对任意n∈N*恒成立,通过研究右边式子的单调性,可得当n=3时,右边的最大值为
对任意n∈N*恒成立,通过研究右边式子的单调性,可得当n=3时,右边的最大值为 ,从而5-λ>
,从而5-λ> ,解之即得λ的取值范围.
,解之即得λ的取值范围.解答:∵n∈N*,∴n+1>0
在不等式2n2-n-3<(5-λ)(n+1)2n两边都除以n+1,得
2n-3<(5-λ)2n对任意n∈N*恒成立,即5-λ>
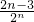
设f(n)=
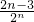 ,可得
,可得当n=1时,
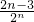 =-
=- <0
<0当n≥2时,
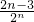 >0,
>0, =
= •
• =
=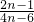
可得
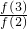 =
= >1,
>1,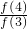 =
= <1,
<1,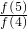 =
= <1,…
<1,…由此可得,f(2)<f(3),f(3)>f(4),f(4)>f(5),…
∴f(n)的最大值为f(3)=
 ,
,要使原不等式对任意n∈N*恒成立,必须5-λ>
 ,解之得λ<
,解之得λ<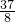
故答案为:λ<
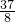
点评:本题给出关于n的式子恒成立,求参数λ的取值范围,着重考查了不等式的基本性质、不等式恒成立和简单的演绎推理等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目