题目内容
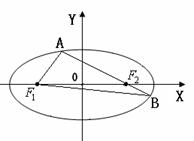如图所示，设点
，
是
的两个焦点，过的直线与椭圆相交于
两点，求△
的面积的最大值，并求出此时直线的方程。
分析：
，设
，
，则
设直线
的方程为
代入椭圆方程得
即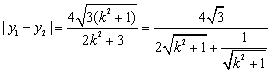
令
，∴
，
（
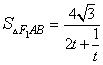）利用均值不等式不能区取“＝”
∴利用
（）的单调性易得在
时取最小值
在即
时取最大值为
，此时直线的方程为
（三角形问题、直线方程、最值问题、函数单调性的综合应用）
练习册系列答案
相关题目
题目内容
如图所示，设点，是的两个焦点，过的直线与椭圆相交于两点，求△的面积的最大值，并求出此时直线的方程。
分析：，设，，则
设直线的方程为代入椭圆方程得
即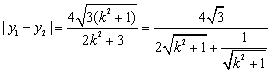
令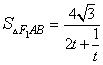，∴，（）利用均值不等式不能区取“＝”
∴利用（）的单调性易得在时取最小值
在即时取最大值为，此时直线的方程为
（三角形问题、直线方程、最值问题、函数单调性的综合应用）
中，
，
，
，
为
的平分线，点
在线段
上，
.如图2所示，将
沿
平面
，连结
，设点
是
平面
；
平面
，其中
为直线
的体积.
中，
，
，
，
为
的平分线，点
在线段
上，
.如图2所示，将
沿
平面
，连结
，设点
是
平面
；
若
平面
，其中
为直线
的体积.