题目内容
数列{an}与{bn}的前n项和分别是An和Bn,且bn=n•an, .
.
(1)求证:数列{an}是从第三项起的等比数列;
(2)当数列{an}是从第一项起的等比数列时,用n的式子表示Bn;
(3)在(2)的条件下,对于给定的自然数k,当n>k时, ,且M∈(-1000,-100),试求k的值.
,且M∈(-1000,-100),试求k的值.
解:(1)证明: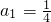 ,当n≥3时,根据an=An-An-1,nan=Bn-Bn-1,可得
,当n≥3时,根据an=An-An-1,nan=Bn-Bn-1,可得 ,即{an}从第三项起成等比.
,即{an}从第三项起成等比.
(2)若{an}从第一项起成等比,那么由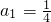 ,
, ,得
,得 ,
, ,
, ,
,
故 .
.
(3)∵ ,又∵
,又∵ ,∴M=-22k,
,∴M=-22k,
由已知M∈(-1000,-100),∴22k∈(100,1000),∴2k=7,8,9,∵k∈N,故k=4为所求.
分析:(1)根据n≥3时,由an=An-An-1,nan=Bn-Bn-1,可得 ,即{an}从第三项起成等比.
,即{an}从第三项起成等比.
(2)若{an}从第一项起成等比,那么由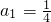 ,
, ,求得 An和Bn.
,求得 An和Bn.
(3)根据 及
及  ,可得 M=-22k,再由22k∈(100,1000),求出k.
,可得 M=-22k,再由22k∈(100,1000),求出k.
点评:本题主要考查等比数列的定义和性质,等比数列的通项公式,求数列极限的方法,求出M=-22k,是解题的难点.
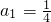 ,当n≥3时,根据an=An-An-1,nan=Bn-Bn-1,可得
,当n≥3时,根据an=An-An-1,nan=Bn-Bn-1,可得 ,即{an}从第三项起成等比.
,即{an}从第三项起成等比.(2)若{an}从第一项起成等比,那么由
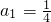 ,
, ,得
,得 ,
, ,
, ,
,故
 .
.(3)∵
 ,又∵
,又∵ ,∴M=-22k,
,∴M=-22k,由已知M∈(-1000,-100),∴22k∈(100,1000),∴2k=7,8,9,∵k∈N,故k=4为所求.
分析:(1)根据n≥3时,由an=An-An-1,nan=Bn-Bn-1,可得
 ,即{an}从第三项起成等比.
,即{an}从第三项起成等比.(2)若{an}从第一项起成等比,那么由
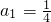 ,
, ,求得 An和Bn.
,求得 An和Bn.(3)根据
 及
及  ,可得 M=-22k,再由22k∈(100,1000),求出k.
,可得 M=-22k,再由22k∈(100,1000),求出k.点评:本题主要考查等比数列的定义和性质,等比数列的通项公式,求数列极限的方法,求出M=-22k,是解题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目