题目内容
一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”，封闭区域边界曲线的长度与区域直径之比称为区域的“周率”，下面四个平面区域（阴影部分）的周率从左到右依次记为τ1，τ2，τ3，τ4，则τ1，τ2，τ3，τ4从大到小的排列为______
第一个图形，其周率相当于一个矩形的周率，此类图形当矩形是正方形时周率最大为2
故τ1=2
；
第二个图形中阴影部分的周长是相应圆周长，其区域直径恰好是直径，故其周率是τ2=π；
第三个图形当把将下折的两段翻上去可以得到一个等边三角形，故其周率是τ3=3；
第四个图形是两个正三角形组合而成的，其周长是正三角形边长的4倍，而其直径是正三角形边长的
倍，其周率是τ4=2
＞π
综上得τ4＞τ2＞τ3＞τ1
故答案为τ4＞τ2＞τ3＞τ1
| 2 |
| 2 |
第二个图形中阴影部分的周长是相应圆周长，其区域直径恰好是直径，故其周率是τ2=π；
第三个图形当把将下折的两段翻上去可以得到一个等边三角形，故其周率是τ3=3；
第四个图形是两个正三角形组合而成的，其周长是正三角形边长的4倍，而其直径是正三角形边长的
2
| ||
| 3 |
| 3 |
综上得τ4＞τ2＞τ3＞τ1
故答案为τ4＞τ2＞τ3＞τ1
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
是平面α内的任意一个封闭区域．现给出如下结论：
；
是平面α内的任意一个封闭区域．现给出如下结论：
是平面
内的任意一个封闭区域.现给出如下结论：
是平面
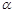内的任意一个封闭区域．现给出如下结论：