题目内容
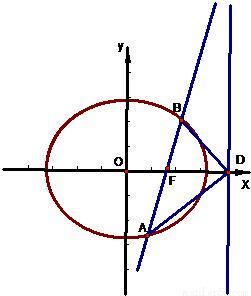
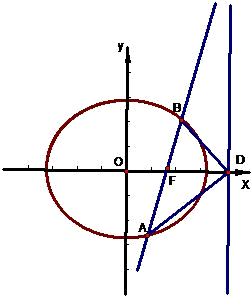 如图,椭圆Q:
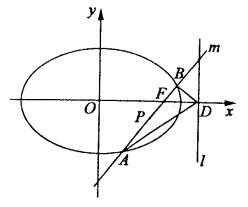
如图,椭圆Q: (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(1)求点P的轨迹H的方程.
(2)在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q≤ ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
 解:如图,(1)设椭圆Q:
解:如图,(1)设椭圆Q: (a>b>0)
(a>b>0)上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),
则

1°当AB不垂直x轴时,x1¹x2,
由(1)-(2)得
b2(x1-x2)2x+a2(y1-y2)2y=0
∴

∴b2x2+a2y2-b2cx=0(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为,椭圆Q右准线l方程是x=
 ,原点距l的距离为
,原点距l的距离为 ,
,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q≤
 )
)则
 =
= =2sin(
=2sin( +
+ )
)当q=
 时,上式达到最大值.
时,上式达到最大值.此时a2=2,b2=1,c=1,D(2,0),|DF|=1
设椭圆Q:
 上的点A(x1,y1)、B(x2,y2),三角形ABD的面积
上的点A(x1,y1)、B(x2,y2),三角形ABD的面积S=
 |y1|+
|y1|+ |y2|=
|y2|= |y1-y2|
|y1-y2|设直线m的方程为x=ky+1,代入
 中,得(2+k2)y2+2ky-1=0
中,得(2+k2)y2+2ky-1=0由韦达定理得y1+y2=
 ,y1y2=
,y1y2= ,
,4S2=(y1-y2)2=(y1+y2)2-4y1y2=

令t=k2+131,
得4S2=
 ,
,当t=1,k=0时取等号.
因此,当直线m绕点F转到垂直x轴位置时,三角形ABD的面积最大.
分析:(1)设出椭圆的标准方程和A,B的坐标进而把A,B代入到椭圆方程联立,先看当当AB不垂直x轴时,方程组中两式相减,进而求得x和y的关系及P的轨迹方程;再看AB垂直于x轴时,点P即为点F,满足刚才所求的方程,最后综合可得答案.
(2)先根据椭圆方程求得其右准线方程,求得原点到右准线的距离,根据c2=a2-b2,求得
 =2sin(
=2sin( +
+ ),进而可知
),进而可知当q=
 时,上式达到最大值.此时a,b和c可求得,则可求得此时的椭圆的方程,设椭圆Q:
时,上式达到最大值.此时a,b和c可求得,则可求得此时的椭圆的方程,设椭圆Q: 上的点A(x1,y1)、B(x2,y2),则可表示出三角形的面积,把直线m的方程代入椭圆方程,消去x,根据韦达定理由韦达定理得y1+y2和y1y2的表达式,进而求得三角形面积的表达式,令t=k2+131,进而求得S关于t的函数,根据t的范围确定三角形面积S的最大值.
上的点A(x1,y1)、B(x2,y2),则可表示出三角形的面积,把直线m的方程代入椭圆方程,消去x,根据韦达定理由韦达定理得y1+y2和y1y2的表达式,进而求得三角形面积的表达式,令t=k2+131,进而求得S关于t的函数,根据t的范围确定三角形面积S的最大值.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了考生运用数学知识分析问题和解决问题的能力.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目


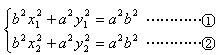 ).
).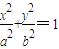 (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.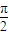 ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?