题目内容
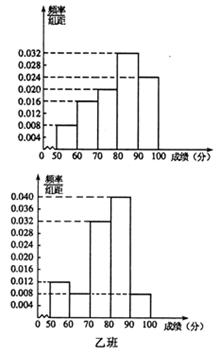
(本小题满分12分)某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.,陈老师采用两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率直方图(如下图).记成绩不低于90分者为“成绩优秀”.
(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的人数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(II)根据频率分布直方图填写下面 列联表,并判断是否有
列联表,并判断是否有 的把握认为:“成绩优秀”与教学方式有关.
的把握认为:“成绩优秀”与教学方式有关.

(I)从乙班随机抽取2名学生的成绩,记“成绩优秀”的人数为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(II)根据频率分布直方图填写下面
 列联表,并判断是否有
列联表,并判断是否有 的把握认为:“成绩优秀”与教学方式有关.
的把握认为:“成绩优秀”与教学方式有关.
(Ⅰ) 的分布列为
的分布列为

 =
=
(Ⅱ)有 的把握认为:“成绩优秀”与教学方式有
的把握认为:“成绩优秀”与教学方式有
 的分布列为
的分布列为
 =
=
(Ⅱ)有
 的把握认为:“成绩优秀”与教学方式有
的把握认为:“成绩优秀”与教学方式有本题主要考查了离散型随机变量的期望和方差、及独立性性检验,属新型的题目,较难.解题的关键是要理解频率分布直方图中每个小矩形的面积即为随机变量落在此区间的概率同时要牢记公式概率=频数/总数
(1)根据题意求出随机变量ξ的所有可能取值为0,1,2然后根据题意求出ξ取每一个值的概率再根据分布列和期望的定义即可得解.
(2)根据频率分布直方图中每个小矩形的面积即为随机变量落在此区间的概率以及概率=频数总数 求出“成绩优秀”的人数和“成绩不优秀”的人数然后即可填表,再利用附的公式求出K2的值再与表中的值比较即可得出结论.
(Ⅰ)解:由频率分布直方图可得“成绩优秀”的人数为4. 的可能值为0,1,2.
的可能值为0,1,2.
 ,
, ,
, ,
,
故 的分布列为
的分布列为

所以 =
=
(Ⅱ)由频率分布直方图可得,甲班成绩优秀、成绩不优秀的人数分别为12、38,乙班成绩优秀、成绩不优秀的人数为4、46
根据列联表数据,得

由于 ,所以有
,所以有 的把握认为:“成绩优秀”与教学方式有
的把握认为:“成绩优秀”与教学方式有
(1)根据题意求出随机变量ξ的所有可能取值为0,1,2然后根据题意求出ξ取每一个值的概率再根据分布列和期望的定义即可得解.
(2)根据频率分布直方图中每个小矩形的面积即为随机变量落在此区间的概率以及概率=频数总数 求出“成绩优秀”的人数和“成绩不优秀”的人数然后即可填表,再利用附的公式求出K2的值再与表中的值比较即可得出结论.
(Ⅰ)解:由频率分布直方图可得“成绩优秀”的人数为4.
 的可能值为0,1,2.
的可能值为0,1,2. ,
, ,
, ,
,故
 的分布列为
的分布列为
所以
 =
=
(Ⅱ)由频率分布直方图可得,甲班成绩优秀、成绩不优秀的人数分别为12、38,乙班成绩优秀、成绩不优秀的人数为4、46
| | 甲班(A方式) | 乙班(B方式) | 总计 |
| 成绩优秀 | 12 | 4 | 16 |
| 成绩不优秀 | 38 | 46 | 84 |
| 总计 | 50 | 50 | 100 |

由于
 ,所以有
,所以有 的把握认为:“成绩优秀”与教学方式有
的把握认为:“成绩优秀”与教学方式有
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 ,其中
,其中 .
.


 <9
<9 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:




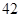


 名,高中学生应该抽取几名?
名,高中学生应该抽取几名? 名,求恰有
名,求恰有 名初中学生的概率.
名初中学生的概率.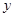 与
与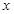 的回归模型中,分别选择了4个不同的模型,它们的相关指数
的回归模型中,分别选择了4个不同的模型,它们的相关指数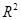 分别为:模型1的相关指数
分别为:模型1的相关指数
 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .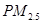 是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,上图是据北京某日早7点至晚8点甲、乙两个
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,上图是据北京某日早7点至晚8点甲、乙两个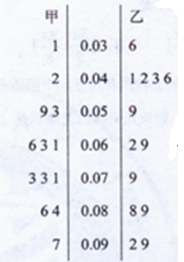
 ,下列判断正确的是
,下列判断正确的是