题目内容
给出下面四个类比结论
①把a(b+c)与ax+y类比,则有ax+y=ax+ay;
②把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny;
③实数a、b,若ab=0,则a=0或b=0;类比向量
、
,若
•
=0,则
=0或
=0;
④向量
,有|
|2=
2;类比复数z,有|z|2=z2.
其中类比结论正确的命题个数为( )
①把a(b+c)与ax+y类比,则有ax+y=ax+ay;
②把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny;
③实数a、b,若ab=0,则a=0或b=0;类比向量
| a |
| b |
| a |
| b |
| a |
| b |
④向量
| a |
| a |
| a |
其中类比结论正确的命题个数为( )
分析:①由指数的运算性质可知,ax+y≠ax+ay;
②由两角和的正弦公式sin(x+y)=sinxcosy+cosxsiny≠sinx+siny;
③由向量的数量积可知
•
=|
||
|cos<
,
>,故可判断③的正误;
④可举例说明④错误.
②由两角和的正弦公式sin(x+y)=sinxcosy+cosxsiny≠sinx+siny;
③由向量的数量积可知
| a |
| b |
| a |
| b |
| a |
| b |
④可举例说明④错误.
解答:解:①由指数的运算性质可知,ax+y=ax•ay≠ax+ay,故①错误;
对于②,∵sin(x+y)=sinxcosy+cosxsiny≠sinx+siny,
∴由a(b+c)与sin(x+y)类比,sin(x+y)=sinx+siny错误;
对于③,∵
•
=|
||
|cos<
,
>,
∴
•
=0⇒
=0,或
=0,或cos<
,
>=0,故③错误;
对于④,不妨令z=1+i,则|z|2=(
)2=2,而z2=(1+i)2=2i,显然|z|2≠z2,故④错误;
综上所述,类比结论正确的命题个数为0.
故答案为:A.
对于②,∵sin(x+y)=sinxcosy+cosxsiny≠sinx+siny,
∴由a(b+c)与sin(x+y)类比,sin(x+y)=sinx+siny错误;
对于③,∵
| a |
| b |
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
| a |
| b |
对于④,不妨令z=1+i,则|z|2=(
| 12+12 |
综上所述,类比结论正确的命题个数为0.
故答案为:A.
点评:本题考查命题的真假判断与应用,着重考查类比推理,掌握指数的运算性质.两角和的正弦、向量的数量积及复数的运算性质是判断的关键,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
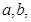 若
若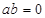 则
则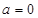 或
或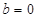 ;类比向量
;类比向量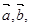 若
若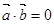 ,则
,则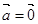 或
或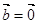
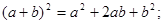 类比向量
类比向量
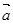 ,有
,有 ;类比复数
;类比复数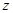 ,有
,有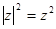
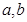 有
有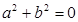 ,则
,则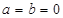 ;类比复数
;类比复数 ,
,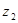 有
有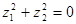 ,则
,则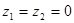
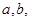 若
若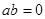 则
则 或
或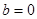 ;类比向量
;类比向量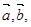 若
若 ,则
,则 或
或
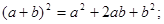 类比向量
类比向量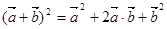
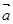 ,有
,有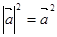 ;类比复数
;类比复数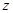 ,有
,有
 有
有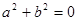 ,则
,则 ;类比复数
;类比复数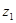 ,
,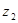 有
有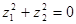 ,则
,则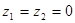
 若
若 则
则 或
或 ;类比向量
;类比向量 若
若 ,则
,则 或
或
 有
有 ,则
,则 ;类比复数
;类比复数 ,
, 有
有 ,则
,则
 类比向量
类比向量
 ,有
,有 ;类比复数
;类比复数