Question

设x，y满足约束条件

x-y≥-1，   x+y≤3，     x≥0，   y≥o，

则z=x-2y的取值范围为

[-3，0]

．

Answer 1

分析：作出不等式组对应的可行域，平移目标直线可知，当直线过点O（0，0），点A（1，2）时，函数z分别取最值，计算可得．

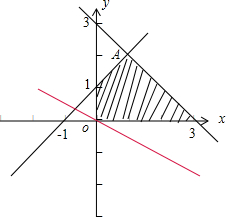
解答：解：作出不等式组对应的可行域，（如图阴影）
平移目标直线z=x-2y可知，当直线过点O（0，0）时，z取最大值0，
当直线过点A（1，2）时，z取最小值-3，
故z=x-2y的取值范围为：[-3，0]
故答案为：[-3，0]

点评：本题考查简单线性规划，准确作图是解决问题的关键，属中档题．