题目内容
对于任意定义在区间D上的函数f(x),若实数x0∈D,满足f(x0)=x0,则称x0为函数f(x)在D上的一个不动点,若f(x)=2x+ +a在区间(0,+∞)上没有不动点,则实数a取值范围是________.
+a在区间(0,+∞)上没有不动点,则实数a取值范围是________.
a>-2
分析:若f(x)=2x+ +a在区间(0,+∞)上没有不动点,则2x+
+a在区间(0,+∞)上没有不动点,则2x+ +a=x在x∈(0,+∞)没有实数解,即
+a=x在x∈(0,+∞)没有实数解,即 +a=0在x∈(0,+∞)没有实数解,
+a=0在x∈(0,+∞)没有实数解,
解答:若f(x)=2x+ +a在区间(0,+∞)上没有不动点,
+a在区间(0,+∞)上没有不动点,
则2x+ +a=x在x∈(0,+∞)没有实数解,即
+a=x在x∈(0,+∞)没有实数解,即 +a=0在x∈(0,+∞)没有实数解,
+a=0在x∈(0,+∞)没有实数解,
分离参数a,得出a=-( ),由于x∈(0,+∞)时,
),由于x∈(0,+∞)时, ≥2,所以-(
≥2,所以-( )≤-2,
)≤-2,
所以a>-2
故答案为:a>-2
点评:本题以新定义为载体,主要考查了一元二次方程的根的求解,及方程的根的分布,考查函数思想及运算求解能力.
分析:若f(x)=2x+
 +a在区间(0,+∞)上没有不动点,则2x+
+a在区间(0,+∞)上没有不动点,则2x+ +a=x在x∈(0,+∞)没有实数解,即
+a=x在x∈(0,+∞)没有实数解,即 +a=0在x∈(0,+∞)没有实数解,
+a=0在x∈(0,+∞)没有实数解,解答:若f(x)=2x+
 +a在区间(0,+∞)上没有不动点,
+a在区间(0,+∞)上没有不动点,则2x+
 +a=x在x∈(0,+∞)没有实数解,即
+a=x在x∈(0,+∞)没有实数解,即 +a=0在x∈(0,+∞)没有实数解,
+a=0在x∈(0,+∞)没有实数解,分离参数a,得出a=-(
 ),由于x∈(0,+∞)时,
),由于x∈(0,+∞)时, ≥2,所以-(
≥2,所以-( )≤-2,
)≤-2,所以a>-2
故答案为:a>-2
点评:本题以新定义为载体,主要考查了一元二次方程的根的求解,及方程的根的分布,考查函数思想及运算求解能力.

练习册系列答案
相关题目
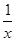 +a在区间(0,+∞)上没有不动点,则实数a取值范围是_______.
+a在区间(0,+∞)上没有不动点,则实数a取值范围是_______.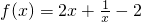 在(0,+∞)上的不动点;
在(0,+∞)上的不动点;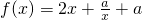 ,在(0,+∞)上没有不动点,求实数a的取值范围.
,在(0,+∞)上没有不动点,求实数a的取值范围.