题目内容
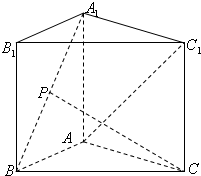已知正三棱柱ABC-A1B1C1的各条棱长都相等，P为A1B上的点，| A1P |
| A1B |
（1）求λ的值；
（2）求异面直线PC与AC1所成角的余弦值．
分析：（1）设出正三棱柱的棱长，以底面上一边的中点为原点建立坐标系，写出要用的各个点的坐标，得到向量的坐标，根据向量的垂直关系，要求的实数的值．
（2）在两条异面直线上构造两个向量，根据两个向量的坐标，写出两个向量的夹角的余弦，是一个负值，根据异面直线所成的角是不大于90°的角，得到余弦值．
（2）在两条异面直线上构造两个向量，根据两个向量的坐标，写出两个向量的夹角的余弦，是一个负值，根据异面直线所成的角是不大于90°的角，得到余弦值．
解答：解：（1）设正三棱柱的棱长为2，建立如图所示的直角坐标系，
则：A（0，-1，0），B(
，0，0)，C（0，1，0），
A1（0，-1，2），
B1(
，0，2)，C1（0，1，2），
∴
=(
，1，0)，
=(0，-2，2)，
=(
，1，-2)，
∵PC⊥AB，
∴
•
=0，(
+
)•
=0，(
+λ
)•
=0，λ=-
=
（2）由（1）知：
=(
，-
，1)，
=(0，2，2)，cos＜
，
＞=
=
=-
，
∴异面直线PC与AC1所成角的余弦值是
．
则：A（0，-1，0），B(
| 3 |
A1（0，-1，2），B1(
| 3 |
∴
| AB |
| 3 |
| CA1 |
| A1B |
| 3 |
∵PC⊥AB，
∴
| CP |
| AB |
| CA1 |
| A1P |
| AB |
| CA1 |
| A1B |
| AB |
| ||||
|
| 1 |
| 2 |
（2）由（1）知：
| CP |
| ||
| 2 |
| 3 |
| 2 |
| AC1 |
| CP |
| AC1 |
| ||||
|
|
| -3+2 | ||
2•2
|
| ||
| 8 |
∴异面直线PC与AC1所成角的余弦值是
| ||
| 8 |
点评：本题考查用空间向量解决立体几何中的夹角和距离的问题，是一个典型的题目，解题的关键是要用的点的坐标比较多，写起来比较繁琐，注意不要出错．
练习册系列答案
阅读快车系列答案
相关题目
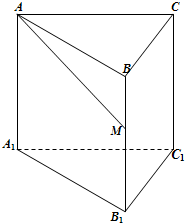如图，已知正三棱柱ABC-A1B1C1的底面边长为1，高为h（h＞2），动点M在侧棱BB1上移动．设AM与侧面BB1C1C所成的角为θ．
已知正三棱柱ABC-A1B1C1的每条棱长均为a，M为棱A1C1上的动点．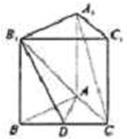
如图，已知正三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=1．
（2009•湖北模拟）如图，已知正三棱柱ABC-A1B1C1各棱长都为a，P为棱A1B上的动点．