题目内容
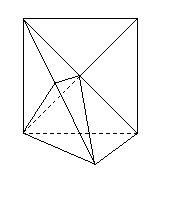
（本小题满分12分）如图，正方形
所在的平面与平面
垂直，
是
和
的交点，
，且
．
| |
平面
； （2）求直线
与平面所成的角的大小；
（3）求二面角
的大小．
(Ⅰ) 见解析 (Ⅱ) 
（Ⅲ）
解析:
| |
| |
是正方形， 
． ………………………1分
∵平面
平面
，又∵
，
平面
． ……………………2分
平面，
．……………3分
平面
． ………………4分
(Ⅱ)连结
，
平面，
是直线
与平面
所成的角． ………5分
设
，则
，
， ………………………6分
， 
．
即直线与平面所成的角为…8分
（Ⅲ）过
作
于
，连结
． ……………………9分
平面，
．
平面
．
是二面角
的平面角． ……10分
∵平面平面，
平面．
．
在
中， ，有
．
由(Ⅱ)所设可得
，
，
． ………………10分
．
．
∴二面角等于． ……………………12分
解法二: ∵四边形是正方形 ，，
∵平面平面，平面， ………2分
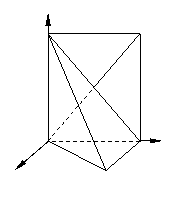
∴可以以点为原点，以过点平行于
的直线为
轴，
分别以直线
和
为
轴和
轴，建立如图所示的空
间直角坐标系
．
设
，则
，
是正方形的对角线的交点，
．……………4分
（Ⅰ）
，
，
，
， ……………………………………4分
平面． ………………5分
（Ⅱ） 平面，
为平面的一个法向量，…………6分
，
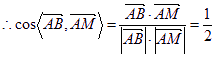．……………7分
．∴直线与平面所成的角为． ……8分
(Ⅲ) 设平面
的法向量为
，则
且
，
且
．
即
取
，则
， 则
．………………10分
又∵
为平面的一个法向量，且
，
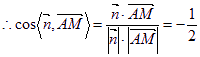，设二面角的平面角为
，则
，
．∴二面角等于．…12分
练习册系列答案
名校课堂系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
