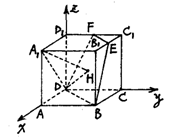
题目内容
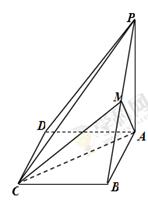
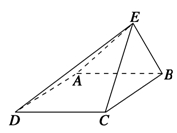
如图,在四棱锥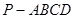 中,
中,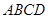 为平行四边形,且
为平行四边形,且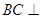 平面
平面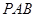 ,
,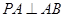 ,
,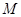 为
为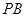 的中点,
的中点,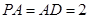 .
.
(Ⅰ) 求证: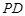 //
//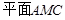 ;
;
(Ⅱ)若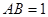 , 求二面角
, 求二面角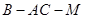 的余弦值.
的余弦值.
(Ⅰ)详见解析;(Ⅱ) .
.
解析试题分析:(Ⅰ)依题意,设 与
与 的交点
的交点 ,说明
,说明 为
为 的中位线,
的中位线, //
//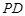 ,从而
,从而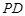 //
//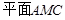 ;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点
;(Ⅱ) 用定义法与向量法求解,用定义法,必须作出二面角的平面角,在利用相似三角形对应边成比例及直角三角形中三角函数的定义求解;用向量法,需要建立恰当的空间直角坐标系,本题以点 为坐标原点,分别以
为坐标原点,分别以 所在直线为
所在直线为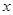 轴,
轴, 轴和
轴和 轴,建立空间直角坐标系
轴,建立空间直角坐标系 最佳,求平面
最佳,求平面 的法向量
的法向量 与平面
与平面 的一个法向量为
的一个法向量为 , 利用公式
, 利用公式 求解.
求解.
试题解析:(Ⅰ)证明: 连接 ,设
,设 与
与 相交于点
相交于点 ,连接
,连接 ,
,
∵ 四边形 是平行四边形,∴点
是平行四边形,∴点 为
为 的中点.
的中点.
∵ 为
为 的中点,∴
的中点,∴ 为
为 的中位线,
的中位线,
∴ //
//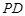 , 2分
, 2分
∵ ,
,
∴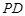 //
//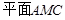 . 4分
. 4分
(Ⅱ) 解法一 : ∵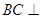 平面
平面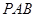 ,
, //
// , 则
, 则 平面
平面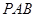 ,故
,故 ,
,
又 , 且
, 且 ,
,
∴  . 6分
. 6分
取 的中点
的中点 ,连接
,连接 ,则
,则 //
// ,且
,且  .
.
∴  .
.
作 ,垂足为
,垂足为 ,连接
,连接 ,由于
,由于 ,且
,且 ,
,
∴ ,∴
,∴  .
.
∴ 为二面角
为二面角 的平面角. 9分
的平面角. 9分
由 ∽
∽ ,得
,得 ,得
,得 ,
,
在 中,
中, .
.
∴ 二面角 的余弦值为
的余弦值为

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
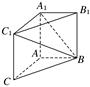
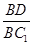 的值.
的值.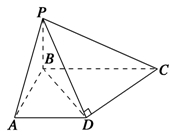
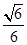 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由. .
.
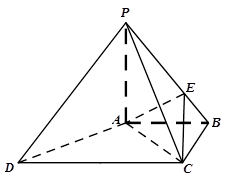
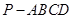 中,
中, ⊥平面
⊥平面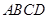 ,底面
,底面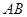 ∥
∥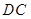 ,
,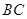 ,
,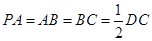 ,点
,点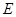 在棱
在棱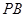 上,且
上,且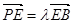 .
.
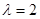 时,求证:
时,求证: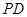 ∥面
∥面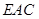 ;
;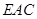 所成角为
所成角为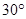 ,求实数
,求实数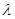 的值.
的值. 中,M,N分别是线段
中,M,N分别是线段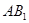 和BD上的点,且AM=BN=
和BD上的点,且AM=BN=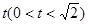
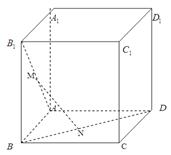
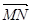 |的最小值;
|的最小值; 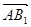 ,
,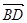 是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.
是否都垂直,如果都垂直给出证明;如果不是都垂直,说明理由.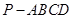 中,
中,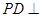 底面
底面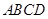 ,底面
,底面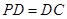 ,
,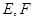 分别是
分别是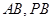 的中点.
的中点.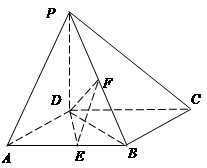
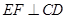 ;
; 内求一点
内求一点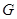 ,使
,使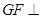 平面
平面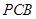 ,并证明你的结论;
,并证明你的结论;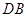 与平面
与平面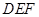 所成角的正弦值.
所成角的正弦值.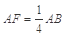 .
.