题目内容
已知f(x)是定义在R上的函数,且f(x)不恒为零,对任意x1,x2∈R,都有f(x1+x2)+f(x1-x2)=2[f(x1)+f(x2)].求证:f(x)是偶函数
答案:
提示:
提示:
若有f(-x)=f(x)(x∈R),则f(x)为偶函数. 观察条件f(x1+x2)+f(x1-x2)=2[f(x1)+f(x2)] 令x1=0,x2=x则f(x)+f(-x)=2[f(0)+f(x)]* 令x2=0,则f(x1)+f(x1)=2[f(x1)+f(0)] ∴ f(0)=0把f(0)=0代入(*)有f(x)=f(-x)问题得证.
|

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 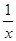 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
