题目内容
函数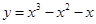 的单调递增区间为______________ 递减区间为____________
的单调递增区间为______________ 递减区间为____________
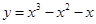 的单调递增区间为______________ 递减区间为____________
的单调递增区间为______________ 递减区间为____________ 和
和 ;
;
试题分析:
 ,令
,令 ,则
,则 ,当
,当 时,
时, ,则
,则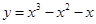 是增函数,当
是增函数,当 时,
时, ,则
,则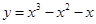 是减函数,所以函数
是减函数,所以函数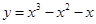 的单调递增区间为
的单调递增区间为 和
和 ,递减区间为
,递减区间为 。
。点评:求函数的单调区间是考试的热点,这类题目一般结合导数都能解决。

练习册系列答案
相关题目
题目内容
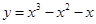 的单调递增区间为______________ 递减区间为____________
的单调递增区间为______________ 递减区间为____________ 和
和 ;
;
 ,令
,令 ,则
,则 ,当
,当 时,
时, ,则
,则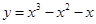 是增函数,当
是增函数,当 时,
时, ,则
,则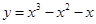 是减函数,所以函数
是减函数,所以函数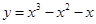 的单调递增区间为
的单调递增区间为 和
和 ,递减区间为
,递减区间为 。
。