题目内容
在四面体PABC中，已知∠APB=∠BPC=∠CPA=| π |
| 2 |
| 2 |
分析：设出PA，PB，PC，求出AB，BC，AC，表示出棱长的和，和体积，利用基本不等式即可求解．
解答：
解：设PA=a，PB=b，PC=c，则AB=
，AC=
，BC=
所以a+b+c+
+
+
=
+1
+1≥3
+3
∴abc≤
四面体体积的最大值为：
（此时a=b=c=
）
故答案为：
解：设PA=a，PB=b，PC=c，则AB=| a2+b2 |
| a2+c2 |
| b2+c2 |
所以a+b+c+
| a2+b2 |
| a2+c2 |
| b2+c2 |
| 2 |
| 2 |
| 3 | abc |
| 2 |
| 3 | abc |
∴abc≤
| 1 |
| 27 |
四面体体积的最大值为：
| 1 |
| 162 |
| 1 |
| 3 |
故答案为：
| 1 |
| 162 |
点评：本题考查棱柱、棱锥、棱台的体积，棱锥的结构特征，基本不等式求最大值，是中档题．
练习册系列答案
相关题目
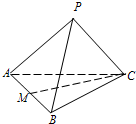在四面体PABC中，各棱长均为2，M为棱AB的中点，则异面直线PA和CM所成角的余弦值为
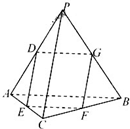如图，在四面体PABC中，PC⊥AB，PA⊥BC，点D，E，F，G分别是棱AP，AC，BC，PB的中点．
如图，在四面体PABC中，点D，E，F，分别是棱AP，AC，BC的中点．
（2012•广州一模）如图，在四面体PABC中，PA=PB，CA=CB，D、E、F、G分别是PA、AC、CB、BP的中点．