Question

【题目】已知椭圆: 的长轴长为4，左、右顶点分别为，经过点的直线与椭圆相交于不同的两点（不与点重合）.

（Ⅰ）当，且直线 轴时， 求四边形的面积；

（Ⅱ）设，直线与直线相交于点，求证：三点共线.

Answer 1

【答案】（Ⅰ）4；（Ⅱ）见解析

【解析】

（Ⅰ）根据条件得，再根据方程得，进而解得坐标，最后根据四边形形状求面积，（Ⅱ）先考虑特殊情形：直线的斜率不存在，具体求出坐标，即得结果，再考虑直线的斜率存在情况，设，，再用坐标表示，以及，最后利用直线方程与椭圆方程联立方程组，结合韦达定理代入化简得.

（Ⅰ）由题意，得， 解得. 所以椭圆方程为.

当，及直线 轴时，易得,. 且,.

所以，，显然此时四边形为菱形，所以四边形的面积为.

（Ⅱ）当直线的斜率不存在时，由题意，得的方程为，

代入椭圆的方程，得，，

易得的方程为.则,,,

所以，即三点共线.

当直线的斜率存在时，设的方程为，，，

联立方程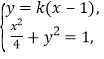 消去y，得.

由题意，得恒成立，故，.

直线的方程为. 令，得.

又因为，，

则直线，的斜率分别为，，

所以.

上式中的分子 ，

所以. 所以三点共线.