题目内容
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC=2,点E为BC的中点,若直线AE与底面BCD所成的角为45°,则三棱锥A-BCD的体积等于( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且DB=DC=2,点E为BC的中点,若直线AE与底面BCD所成的角为45°,则三棱锥A-BCD的体积等于( )分析:确定∠AED为直线AE与底面BCD所成的角,求出DE,可得AD,再利用三棱锥A-BCD的体积公式,即可得到结论.
解答:解:∵DB=DC=2,点E为BC的中点,∴DE⊥BC,DE=
∵DA,DB,DC两两垂直,∴AD⊥平面DBC,
∴∠AED为直线AE与底面BCD所成的角
∵直线AE与底面BCD所成的角为45°,∴∠AED=45°,
∴AD=DE=
∴三棱锥A-BCD的体积等于
×
×2×2×
=
故选D.
| 2 |
∵DA,DB,DC两两垂直,∴AD⊥平面DBC,
∴∠AED为直线AE与底面BCD所成的角
∵直线AE与底面BCD所成的角为45°,∴∠AED=45°,
∴AD=DE=
| 2 |
∴三棱锥A-BCD的体积等于
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
2
| ||
| 3 |
故选D.
点评:本题考查线面角,考查三棱锥A-BCD的体积,考查学生的计算能力,属于基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
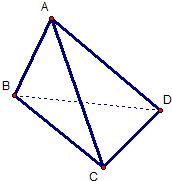 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=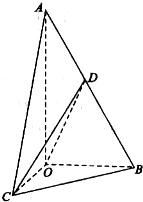 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,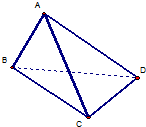 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=