题目内容
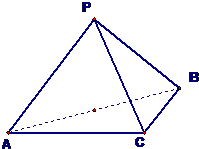 三棱锥P-ABC中,PA=PB=PC,∠ACB=90°,AC=CB=2.
三棱锥P-ABC中,PA=PB=PC,∠ACB=90°,AC=CB=2.(Ⅰ)求证:平面PAB⊥平面ABC;
(Ⅱ)若
| CB |
| AD |
分析:(Ⅰ)作PO⊥平面ABC于点O,由PA=PB=PC,知O为△ABC的外心,由∠ACB=90°,知O为AB边的中点,由此能够证明平面PAB⊥平面ABC.
(Ⅱ)以O为坐标原点,以OA为x轴,以OC为y轴,以OP为z轴,建立空间直角坐标系利用向量法能够求出二面角P-CD-A的余弦值.
(Ⅱ)以O为坐标原点,以OA为x轴,以OC为y轴,以OP为z轴,建立空间直角坐标系利用向量法能够求出二面角P-CD-A的余弦值.
解答:证明:(Ⅰ)作PO⊥平面ABC于点O,
∵PA=PB=PC,
∴OA=OB=OC,即O为△ABC的外心
又∵△ABC中,∠ACB=90°,∴O为AB边的中点,
∴PO?平面PAB,
∴平面PAB⊥平面ABC.…(6分)
(Ⅱ)∵△ABC中,∠ACB=
,AC=CB=2,
∴OA=OB=OC=
∵
=2
,且异面直线PC与AD的夹角为60°,PB=PC
∴∠PCB=60°,∴△PCB为正三角形,解得PO=
.
以O为坐标原点,以OA为x轴,以OC为y轴,以OP为z轴,
建立如图所示空间直角坐标系O-xyz,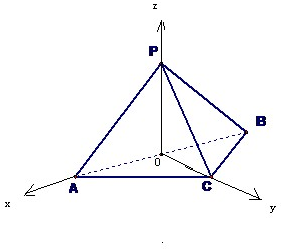
则A(
,0,0),B(-
,0,0),C(0,
,0),P(0,0,
),
∵
=(-
,-
,0)=2
,∴D(
,-
,0). …(9分)
设平面PCD的法向量为
=(x,y,z),
∵
=(0,-
,
),
=(
,
,0)
由
,取
=(3,1,1)
平面ACD的法向量为
=(0,0,
)
∴cos<
,
>=
=
=
.
由图可知,所求二面角P-CD-A为钝角,其的余弦值为-
.…(12分)
∵PA=PB=PC,
∴OA=OB=OC,即O为△ABC的外心
又∵△ABC中,∠ACB=90°,∴O为AB边的中点,
∴PO?平面PAB,
∴平面PAB⊥平面ABC.…(6分)
(Ⅱ)∵△ABC中,∠ACB=
| π |
| 2 |
∴OA=OB=OC=
| 2 |
∵
| CB |
| AD |
∴∠PCB=60°,∴△PCB为正三角形,解得PO=
| 2 |
以O为坐标原点,以OA为x轴,以OC为y轴,以OP为z轴,
建立如图所示空间直角坐标系O-xyz,

则A(
| 2 |
| 2 |
| 2 |
| 2 |
∵
| CB |
| 2 |
| 2 |
| AD |
| ||
| 2 |
| ||
| 2 |
设平面PCD的法向量为
| n |
∵
| CP |
| 2 |
| 2 |
| CD |
| ||
| 2 |
-3
| ||
| 2 |
由
|
| n |
平面ACD的法向量为
| OP |
| 2 |
∴cos<
| OP |
| n |
| ||||
|
|
| 1 | ||
|
| ||
| 11 |
由图可知,所求二面角P-CD-A为钝角,其的余弦值为-
| ||
| 11 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意向量法的合理运用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.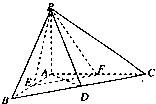 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,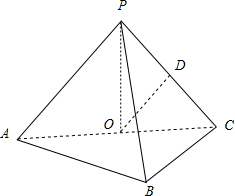 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.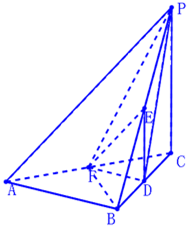 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.