题目内容
当x,y满足 (k为常数)时,使z=x+3y的最大值为12的k值为
(k为常数)时,使z=x+3y的最大值为12的k值为
- A.-9
- B.9
- C.-12
- D.12
A
分析:画出 的可行域,将目标函数变形,画出其相应的直线,当直线平移至固定点时,z最大,求出最大值列出方程求出k的值
的可行域,将目标函数变形,画出其相应的直线,当直线平移至固定点时,z最大,求出最大值列出方程求出k的值
解答: 解:画出
解:画出  的平面区域,
的平面区域,
将目标函数变形为y=- x+
x+ z,画出其相应的直线,
z,画出其相应的直线,
由 得
得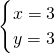
当直线y=- x+
x+ z平移至A(3,3)时z最大为12,
z平移至A(3,3)时z最大为12,
将x=3,y=3代入直线2x+y+k=0得:
k=-9
故选A.
点评:本小题主要考查简单线性规划、不等式组表示平面区域等基础知识,考查运算求解能力,考查数形结合思想.属于基础题.
分析:画出
 的可行域,将目标函数变形,画出其相应的直线,当直线平移至固定点时,z最大,求出最大值列出方程求出k的值
的可行域,将目标函数变形,画出其相应的直线,当直线平移至固定点时,z最大,求出最大值列出方程求出k的值解答:
 解:画出
解:画出  的平面区域,
的平面区域,将目标函数变形为y=-
 x+
x+ z,画出其相应的直线,
z,画出其相应的直线,由
 得
得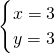
当直线y=-
 x+
x+ z平移至A(3,3)时z最大为12,
z平移至A(3,3)时z最大为12,将x=3,y=3代入直线2x+y+k=0得:
k=-9
故选A.
点评:本小题主要考查简单线性规划、不等式组表示平面区域等基础知识,考查运算求解能力,考查数形结合思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知定义在R上的函数f(x)满足f(2-x)+f(x)=0和f(x-2)+f(x)=0,且当x∈[1,2]时f(x)=1-(x-2)2.若直线y=kx(k为常数),与函数f(x)的图象在区间(-2,5)上恰有4个公共点,则实数k的取值范围是( )
A、(2
| ||
B、(2
| ||
C、(-
| ||
D、(-
|
 (k为常数)时,使得z=x+3y的最大值为12,则k=________.
(k为常数)时,使得z=x+3y的最大值为12,则k=________. 为常数)时,能使z=x+3y的最大值为12,则k= .
为常数)时,能使z=x+3y的最大值为12,则k= .