题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() ,在数列
,在数列![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 是等比数列;
是等比数列;
(2)若![]() ,求数列
,求数列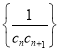 的前
的前![]() 项和
项和![]() ;
;
(3)求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)利用递推关系可得![]() ,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得
,由等比数列的定义即可得出结论;(2)利用对数的运算性质可得![]() ,根据裂项求和方法即可得出;(3)
,根据裂项求和方法即可得出;(3)![]() 时,
时, ![]() 时,
时, ![]() ,综上
,综上![]() ,可得
,可得![]() ,再利用错位相减法及分组求和法即可得结果.
,再利用错位相减法及分组求和法即可得结果.
试题解析:(1) 证明: ![]() 且
且![]()
![]()
![]() 是首项为4,公比为2的等比数列 .
是首项为4,公比为2的等比数列 .
(2) 由(1)知 ![]() ,
,
所以 ![]() ,
,
则![]()
![]() ,
,
![]()
![]() .
.
(3) ![]() 时
时 ![]() ,
,
![]() 时
时 ![]() ,
,
综上 ![]() ,
,
![]() ,解得
,解得
![]() .
.
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④![]()
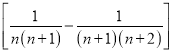 ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.

练习册系列答案
相关题目