题目内容
已知函数
，若f′（x）=0在（1，3]上有解，则实数a的取值范围为________．
-7≤a＜-1
分析：对函数求导，根据f′（x）=0在（1，3]上有解，即2a-1=-x2-2x=-（x+1）2+1在（1，3]上有解，转化为求函数y=-（x+1）2+1在（1，3]上的值域，进而解不等式-15≤2a-1＜-3即可求得数a的取值范围．
解答：f′（x）=x2+2x+（2a-1），
∵f′（x）=0在（1，3]上有解，
∴2a-1=-x2-2x=-（x+1）2+1在（1，3]上有解，
而y=-（x+1）2+1在（1，3]上的y＜-3，最小值为-15，
∴-15≤2a-1＜-3，解得-7≤a＜-1，
故答案为：-7≤a＜-1．
点评：此题是中档题．考查函数零点与方程根的关系，以及导数的运算和基本初等函数的导数，体现了转化的思想，考查学生分析解决问题的能力和计算能力．
分析：对函数求导，根据f′（x）=0在（1，3]上有解，即2a-1=-x2-2x=-（x+1）2+1在（1，3]上有解，转化为求函数y=-（x+1）2+1在（1，3]上的值域，进而解不等式-15≤2a-1＜-3即可求得数a的取值范围．
解答：f′（x）=x2+2x+（2a-1），
∵f′（x）=0在（1，3]上有解，
∴2a-1=-x2-2x=-（x+1）2+1在（1，3]上有解，
而y=-（x+1）2+1在（1，3]上的y＜-3，最小值为-15，
∴-15≤2a-1＜-3，解得-7≤a＜-1，
故答案为：-7≤a＜-1．
点评：此题是中档题．考查函数零点与方程根的关系，以及导数的运算和基本初等函数的导数，体现了转化的思想，考查学生分析解决问题的能力和计算能力．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
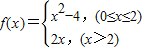，若f（x）=12，则x= ．
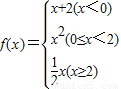，若f（x）=2，则x的值为（ ）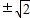
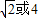
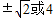
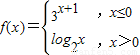，若f（x）≥1，则x的取值范围为 ．
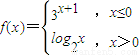，若f（x）≥1，则x的取值范围为 ．
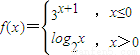，若f（x）≥1，则x的取值范围为 ．