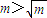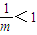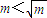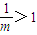题目内容
lgm>0的一个必要不充分条件是( )
A、m>
| ||
B、
| ||
C、m<
| ||
D、
|
分析:要求lgm>0的必要不充分条件,即求一个集合M使,不等式lgm>0的解集A?M,我们对答案中的四个不等式分别求解,对于A:m>1;对于B:m<0或m>1;对于C:0<m<1;对于D:0<m<1;再进行充要条件的判断,即可得到答案.
解答:解:若lgm>0,则m>1
则有(B)
<1,(A)m>
,成立,反之,
而当m>
时,lgm>0也成立,故m>
是lgm>0的充要条件;(B)正确;
而当
<1时,m还可能小于0,此时lgm>0无意义,故
<1不是lgm>0的充要条件,(A)错;
对于(C)和(D):都是得到:0<m<1.
故(C)和(D)都不是lgm>0的必要不充分条件.
故选B
则有(B)
| 1 |
| m |
| m |
而当m>
| m |
| m |
而当
| 1 |
| m |
| 1 |
| m |
对于(C)和(D):都是得到:0<m<1.
故(C)和(D)都不是lgm>0的必要不充分条件.
故选B
点评:判断充要条件的方法是:①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
lgm>0的一个必要不充分条件是:( )
A、m>
| ||||||
B、
| ||||||
C、
| ||||||
D、
|