题目内容
如图，偶函数f（x）的图象形如字母M，奇函数g（x）的图象形如字母N，若方程：f（f（x））=0，f（g（x））=0，g（g（x））=0，g（f（x））=0的实根个数分别为a、b、c、d，则a+b+c+d=（ ）
分析：结合函数图象把方程根的个数转化为函数图象的交点个数，可分别求得a，b，c，d，进而可得答案．
解答：解：由图象知，f（x）=0有三个根，0，±
，由f（f（x））=0知f（x）=0或±
．而f（x）=±
无解，∴a=3．
同理，由f（g（x））=0，得g（x）=0或±
，由图象可知g（x）所对每一个值都能有三个根，因而b=9；
由图象知g（x）=0，有三个根，0，还有一组相反数，不妨设为±
．由g（g（x））=0，知g（x）=0或±
，由上面分析，可知，c=9，
由g（f（x））=0，知f（x）=0 或±
，由图象可可以看出0时对应有三个根，而
时有四个，而-
时只有两个，加在一起也是9个，d=9，
∴a+b+c+d=30，
故选B．
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
同理，由f（g（x））=0，得g（x）=0或±
| 3 |
| 2 |
由图象知g（x）=0，有三个根，0，还有一组相反数，不妨设为±
| 3 |
| 4 |
| 3 |
| 4 |
由g（f（x））=0，知f（x）=0 或±
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴a+b+c+d=30，
故选B．
点评：本题考查函数函数的图象及其应用，考查方程根的个数，考查数形结合思想．
练习册系列答案
相关题目
（2013•海口二模）设偶函数f（x）=Asin（ωx+?）（A＞0，ω＞0，0＜?＜π）的部分图象如图所示，△KLM为等腰直角三角形，∠KML=90°，KL=1，则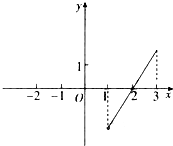
已知定义在[-3，-1）∪（1，3]上的偶函数f（x）的图象过点（2，0），当x＞0时f（x）的图象如图所示，那么不等式f（x）＞0的解集是
