题目内容
4．若复数z=m（m+1）+（m+1）i（i为虚数单位）是纯虚数，则实数m的值为0．分析 根据复数为纯虚数的概念，得到复数的实部为0，并且虚部不为0求出m．
解答 解：因为复数z=m（m+1）+（m+1）i（i为虚数单位）是纯虚数，所以$\left\{\begin{array}{l}{m（m+1）=0}\\{m+1≠0}\end{array}\right.$，解得m=0；
故答案为：0．
点评 本题考查了复数的基本概念；如果复数a+bi（a，b是实数）是纯虚数，那么a=0并且b≠0．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
14．已知m∈R，函数f（x）=$\left\{\begin{array}{l}{|3x+1|，x＜0}\\{lo{g}_{3}x，x＞0}\end{array}\right.$，g（x）=x2-2x+2m-1，若函数y=f（g（x））-m有6个零点，则实数m的取值范围是（ ）
| A． | （0，$\frac{5}{7}$） | B． | （$\frac{3}{7}$，$\frac{5}{7}$） | C． | （0，$\frac{3}{7}$） | D． | （$\frac{2}{7}$，1） |
15．已知等比数列{an}中a2=2，a5=$\frac{1}{4}$，则a1•a2+a2•a3+a3•a4+…+an•an+1等于（ ）
| A． | 16（1-4-n） | B． | 16（1-2n） | C． | $\frac{32}{3}（1-{4^{-n}}）$ | D． | $\frac{32}{3}（1-{2^{-n}}）$ |
12．已知函数f（x）=$\left\{\begin{array}{l}{x+1，x≤1}\\{-x+3，x＞1}\end{array}\right.$，那么f（f（$\frac{5}{2}$））=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{2}$ | C． | $\frac{5}{2}$ | D． | $\frac{7}{2}$ |
9．已知cosθ＞0，tanθ＜0，则$\sqrt{1-co{s}^{2}θ}$化简结果为（ ）
| A． | ±sinθ | B． | sinθ | C． | -sinθ | D． | 以上都不对 |
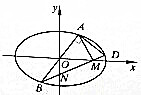对于椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），c为椭圆半焦距，e为椭圆离心率，过原点O的直线与椭圆C交于A、B两点（A、B不是椭圆C的顶点），点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M、N两点，证明：