题目内容
如图,在棱长为 的正方体
的正方体 的对角线
的对角线 上任取一点
上任取一点 ,以
,以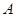 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数 的图象最有可能的是( )
的图象最有可能的是( )
B
解析试题分析:分析:当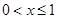 ,以
,以 为半径的球面与正方体
为半径的球面与正方体 的侧面
的侧面 、
、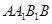 以及下底面
以及下底面 均相交,且与侧面
均相交,且与侧面 、
、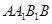 以及下底面
以及下底面 的交线均为圆心角为
的交线均为圆心角为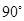 的圆弧,即
的圆弧,即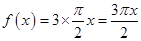 ,此时函数
,此时函数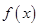 是关于自变量
是关于自变量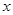 的正比例函数,排除选项
的正比例函数,排除选项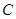 、
、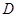 ,当
,当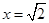 时,侧面
时,侧面 、
、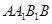 以及下底面
以及下底面 内的点到点
内的点到点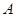 的最大距离为
的最大距离为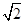 ,此时球面与这三个面无交线,考虑球面与平面
,此时球面与这三个面无交线,考虑球面与平面 的交线,设球面与平面
的交线,设球面与平面 的交线是半径为
的交线是半径为 的圆弧,在圆弧上任取一点
的圆弧,在圆弧上任取一点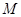 ,则
,则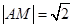 ,
, ,易知,
,易知,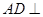 平面
平面 ,由于
,由于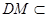 平面
平面 ,
, ,由勾股定理得
,由勾股定理得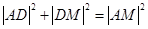 ,则有
,则有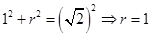 ,即球面与正方体的侧面
,即球面与正方体的侧面 的交线为以
的交线为以 为半径,且圆心角为
为半径,且圆心角为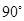 的圆弧,同理,球面与侧面
的圆弧,同理,球面与侧面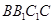 及底面
及底面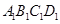 的交线都是以
的交线都是以 为半径,且圆心角为
为半径,且圆心角为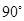 的圆弧,即
的圆弧,即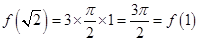 ,排除
,排除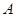 选项,故选项
选项,故选项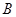 正确.
正确.
考点:1弧长公式;2函数图像及表示法。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 ,
, ,则( )
,则( )
A. 与 与 均为偶函数 均为偶函数 | B. 为奇函数, 为奇函数, 为偶函数 为偶函数 |
C. 与 与 均为奇函数 均为奇函数 | D. 为偶函数, 为偶函数, 为奇函数 为奇函数 |
在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x)(实线表示),另一种是平均价格曲线y=g(x)(虚线表示)(如f(2)=3是指开始买卖后两个小时的即时价格为3元g(2)=3表示2个小时内的平均价格为3元),下图给出四个图象: 
其中可能正确的图象序号是 .
| A.①②③④ | B.①③④ | C.①③ | D.③ |
函数f(x)= 的定义域为( )
的定义域为( )
| A.(0,+∞) | B.(1,+∞) |
| C.(0,1) | D.(0,1)∪(1,+∞) |
函数f(x)=-|x-5|+2x-1的零点所在的区间是( )
| A.(0,1) | B.(1,2) |
| C.(2,3) | D.(3,4) |
函数f(x)= 的定义域是( )
的定义域是( )
| A.[-3,3] | B.[- |
| C.(1, | D.[- |
函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…,xn,使得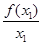 =
= =…=
=…= ,则n的取值范围为( ).
,则n的取值范围为( ).
| A.{3,4} | B.{2,3,4} | C.{3,4,5} | D.{2,3} |
函数y= 的定义域是 ( ).
的定义域是 ( ).
A.[- ,-1)∪(1, ,-1)∪(1, ] ] | B.(- ,-1)∪(1, ,-1)∪(1, ) ) |
| C.[-2,-1)∪(1,2] | D.(-2,-1)∪(1,2) |