题目内容
己知数列为等差数列,且a5+a7+a9=4π,则tan(a6+a8)的值为
- A.

- B.-

- C.±

- D.-

B
分析:由等差数列的性质可知,a5+a7+a9=3a7=4π,可求a7,代入tan(a6+a8)=tan2a7即可求解
解答:由等差数列的性质可知,a5+a7+a9=3a7=4π,
∴
则tan(a6+a8)=tan2a7=tan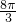 =-
=-
故选B
点评:本题主要考查了等差数列的 性质及特殊角的正切函数值的求解,属于基础试题
分析:由等差数列的性质可知,a5+a7+a9=3a7=4π,可求a7,代入tan(a6+a8)=tan2a7即可求解
解答:由等差数列的性质可知,a5+a7+a9=3a7=4π,
∴

则tan(a6+a8)=tan2a7=tan
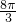 =-
=-
故选B
点评:本题主要考查了等差数列的 性质及特殊角的正切函数值的求解,属于基础试题

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目







