题目内容
设f(x)是定义在R上的不恒为零的函数,且对于任意的a,b∈R满足f(ab)-af(b)=bf(a), .有下列结论:
.有下列结论:
①f(1)=f(0)=0;
②f(x)为偶函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.其中正确的是
- A.①②③
- B.①②④
- C.①③④
- D.②③④
C
分析:给a、b赋值,使它们都等于0,再使它们都等于1,得到结论①正确;由f(1)=-f(-1)-f(-1)=0,得f(-1)=0,f(-x)=-f(x)+xf(-1)=-f(x),所以f(x)是R上的奇函数;根据f(ab)-af(b)=bf(a),可得 =
= +
+ +…+
+…+ (共n个)=n,从而f(3n)=n×3n,由此可得③④正确.
(共n个)=n,从而f(3n)=n×3n,由此可得③④正确.
解答:①∵取a=b=0,可得f(0)=0,取a=b=1,可得f(1)=0,∴f(0)=f(1)=0,即①正确;
②∵f(1)=-f(-1)-f(-1)=0,∴f(-1)=0,∴f(-x)=-f(x)+xf(-1)=-f(x),∴f(x)是R上的奇函数.故②不正确;
③∵f(ab)-af(b)=bf(a),∴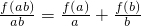 ,∴
,∴ ,
,
以此类推 =
= +
+ +…+
+…+ (共n个)=n,
(共n个)=n,
∴f(3n)=n×3n,∴an= =n,故③正确.
=n,故③正确.
④bn= =3n,故④正确.
=3n,故④正确.
∴正确的是①③④.
故选C.
点评:本题考查了数列与函数知识的综合运用,解题时应用了函数的赋值法,函数的奇偶性,等差、等比数列的定义等知识,要细心解答.
分析:给a、b赋值,使它们都等于0,再使它们都等于1,得到结论①正确;由f(1)=-f(-1)-f(-1)=0,得f(-1)=0,f(-x)=-f(x)+xf(-1)=-f(x),所以f(x)是R上的奇函数;根据f(ab)-af(b)=bf(a),可得
 =
= +
+ +…+
+…+ (共n个)=n,从而f(3n)=n×3n,由此可得③④正确.
(共n个)=n,从而f(3n)=n×3n,由此可得③④正确.解答:①∵取a=b=0,可得f(0)=0,取a=b=1,可得f(1)=0,∴f(0)=f(1)=0,即①正确;
②∵f(1)=-f(-1)-f(-1)=0,∴f(-1)=0,∴f(-x)=-f(x)+xf(-1)=-f(x),∴f(x)是R上的奇函数.故②不正确;
③∵f(ab)-af(b)=bf(a),∴
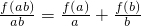 ,∴
,∴ ,
,以此类推
 =
= +
+ +…+
+…+ (共n个)=n,
(共n个)=n,∴f(3n)=n×3n,∴an=
 =n,故③正确.
=n,故③正确.④bn=
 =3n,故④正确.
=3n,故④正确.∴正确的是①③④.
故选C.
点评:本题考查了数列与函数知识的综合运用,解题时应用了函数的赋值法,函数的奇偶性,等差、等比数列的定义等知识,要细心解答.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |