题目内容
(08年咸阳市二模) 过抛物线![]()
![]()
![]() 的对称轴上的定点
的对称轴上的定点![]() ,作直线
,作直线![]() 与抛物线相交于
与抛物线相交于![]() 两点.
两点.
(1)试证明![]() 两点的纵坐标之积为定值;
两点的纵坐标之积为定值;
(2)若点![]() 是定直线
是定直线![]() 上的任一点,试探索三条直线
上的任一点,试探索三条直线![]() 的斜率之间的关系,并给出证明.
的斜率之间的关系,并给出证明.

解析:(1)证明:.设![]() 有
有![]() ,下证之:
,下证之:
设直线![]() 的方程为:
的方程为:![]() 与
与![]() 联立得
联立得
![]()
![]()
![]()
消去![]() 得
得![]()
由韦达定理得![]()
![]() ,
,
(2)解:三条直线![]() 的斜率成等差数列,下证之:
的斜率成等差数列,下证之:
设点![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ;
;
直线![]() 的斜率为
的斜率为![]()
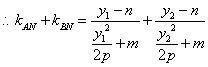
![]()
![]()
![]()
又![]() 直线
直线![]() 的斜率为
的斜率为![]()
![]()
即直线![]() 的斜率成等差数列.
的斜率成等差数列.

练习册系列答案
相关题目