题目内容
(本小题满分10分) 定义域为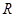 的奇函数
的奇函数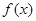 满足
满足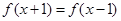 ,且当
,且当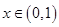 时,
时,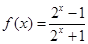 .
.
(1)求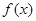 在
在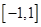 上的解析式;
上的解析式;
(2)当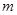 取何值时,方程
取何值时,方程 在
在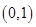 上有解?
上有解?
【答案】
解:(1) . (2)
. (2) .
.
【解析】本试题主要考查了运用函数的奇偶性来进行函数解析式的求解,以及函数与方程根的问题的综合运用。采用图像与图像的交点来分析可得。
(1)利用当当 时,
时, ,
,
由 为
为 上的奇函数,得
上的奇函数,得 ,便可以得到解析式。对于x=0处,函数值必然为零。
,便可以得到解析式。对于x=0处,函数值必然为零。
(2)借助于指数函数的值域,可以得到 ,参数m的范围。
,参数m的范围。
解:(1)当 时,
时, ,
,
由 为
为 上的奇函数,得
上的奇函数,得 ,
,
∴ .………………………………… 3分
.………………………………… 3分
又由奇函数得 .
.
 ,
,
 .
.
 . ……………………………………………………5分
. ……………………………………………………5分
(2) ,
,
 ,
,

 ,
, .
.
即 . ………………………………………………………………10分
. ………………………………………………………………10分

练习册系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,