题目内容
(满分12分)已知椭圆中心在原点,焦点在![]() 轴上,一个顶点为A(0,-1),且其右焦点到直线
轴上,一个顶点为A(0,-1),且其右焦点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)是否存在斜率为![]() 的直线
的直线![]() ,使
,使![]() 与已知椭圆交于不同的两点
与已知椭圆交于不同的两点![]() ,
,
且![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(1)因为椭圆中心在原点,焦点在x轴上,一个顶点为A(0,-1),
由题意,可设椭圆的方程为![]() ,则其右焦点为
,则其右焦点为![]()
所以![]() 到直线
到直线![]() 的距离为
的距离为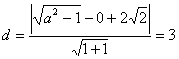 ,解得
,解得![]()
所以椭圆的方程为![]() (4分)
(4分)
(2)设存在满足条件的直线![]() ,设其方程为
,设其方程为![]()
![]()
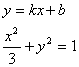 由方程组消去
由方程组消去![]() ,得方程
,得方程![]() ① (6分)
① (6分)
设![]() ,其中
,其中![]() 是方程①的两个根,
是方程①的两个根,
因为 ![]() , 关于
, 关于![]() 的二次方程的判别式
的二次方程的判别式
![]() ,即
,即 ![]() ②
②
由一元二次方程根与系数的关系得![]()
![]()
![]() 的中点P的坐标为
的中点P的坐标为![]() (9分)
(9分)
因为![]() ,所以
,所以![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]()
于是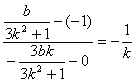 得
得![]() 代入②并整理得
代入②并整理得![]()
![]()
故存在满足条件的直线![]() ,其斜率的取值范围为
,其斜率的取值范围为![]() 且
且![]() 。 (12分)
。 (12分)

练习册系列答案
相关题目
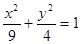 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点.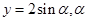 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;