题目内容
设a∈R,函数f(x)=x2-ax+2,
(Ⅰ)若a=3,解不等式f(x)<0;
(Ⅱ)若f(x)>0恒成立,求a的取值范围。
(Ⅰ)若a=3,解不等式f(x)<0;
(Ⅱ)若f(x)>0恒成立,求a的取值范围。
解:(Ⅰ)因为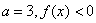 ,
,
所以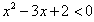 ,
,
解得1<x<2,
所以不等式的解集为{x|1<x<2}。
(Ⅱ)因为f(x)>0恒成立,即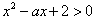 恒成立,
恒成立,
所以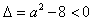 ,
,
所以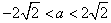 ,
,
所以a的取值范围是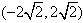 。
。
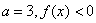 ,
,所以
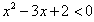 ,
,解得1<x<2,
所以不等式的解集为{x|1<x<2}。
(Ⅱ)因为f(x)>0恒成立,即
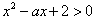 恒成立,
恒成立,所以
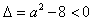 ,
,所以
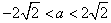 ,
,所以a的取值范围是
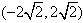 。
。 
练习册系列答案
相关题目
设a∈R,函数f(x)=ex-ae-x的导函数为f′(x),且f′(x)是奇函数,则a=( )
| A、0 | B、1 | C、2 | D、-1 |