Question

（12分）如图，三棱锥P—ABC中，△ABC是正三角形，，D为PA的中点，二面角P—AC—B为120°，PC = 2，AB=2.

（Ⅰ）求证：AC⊥BD；

（Ⅱ）求BD与底面ABC所成角的正弦值.

                               

Answer 1

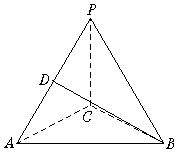
（12分）证明：解:（Ⅰ）取AC中点E，连结DE、BE，

则DE∥PC，PC⊥AC,

∴DE⊥AC……………………………………………………………3分 

又△ABC是正三角形，∴BE⊥AC,∴AC⊥平面DEB.

又BD平面BED,∴AC⊥BD……………………………………….7分 

（Ⅱ）由（Ⅰ）中知DE⊥AC，BE⊥AC,

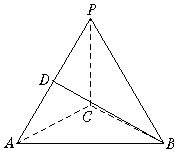
∴∠DEB是二面角P—AC—B的平面角.

∴∠DEB=120°.又AB=2,其中线BE=AB=3，DE=PC=1.

∵AC⊥平面BDE，

又AC平面ABC,

∴平面ABC⊥平面BDE……………………………………………..9分

且交线为BE，过D作平面ABC的垂线DF，垂足F必在直线BE上.

又∠DEB=120°，

∴设F在BE延长线上，则∠DBE即为BD与底面ABC所成的角…10分 

又△DEB中，DB²=DE²+BE²－2BE·DEcos120°=13,

∴BD=.由正弦定理：,

∴sinDBE=,即BD与底面ABC所成的角的正弦值为…………12分