题目内容
有四个函数：①y=sin2x ②y=|sinx|③y=sin|x|④y=2sinx，其中周期是π，且在（0，
）是增函数的函数个数是（ ）A．1
B．2
C．3
D．0
【答案】分析：首先对y=sin2x 化简可得y=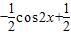
，再结合题意分别画出①②函数的图象，根据图象可得它们符合题意，③④可以根据正弦函数的图象可得③不具有周期性，④的周期为2π．
解答：解：①由y=sin2x 可得y=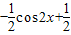
，所以函数的周期为π，并且函数的图象为：
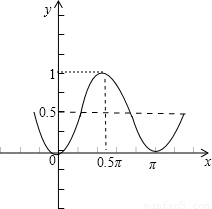
所以在（0，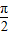
）是增函数．所以①正确．
②y=|sinx|的图象为
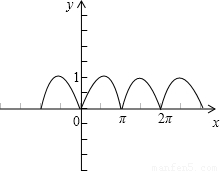
所以在（0，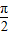
）是增函数，并且函数的周期为π．所以②正确．
③y=sin|x|时偶函数，并且其图象在（0，+∞）上的图象与正弦函数的图象一致，所以函数不具有周期性．所以③错误．
④y=2sinx的周期为2π．所以④错误．
点评：本题主要考查带绝对值的三角函数的图象和性质的应用．考查三角函数的周期性和单调性，三角函数的图象是高考的重点，一定要会画图．
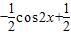，再结合题意分别画出①②函数的图象，根据图象可得它们符合题意，③④可以根据正弦函数的图象可得③不具有周期性，④的周期为2π．解答：解：①由y=sin2x 可得y=
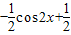，所以函数的周期为π，并且函数的图象为：所以在（0，
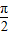）是增函数．所以①正确．②y=|sinx|的图象为
所以在（0，
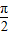）是增函数，并且函数的周期为π．所以②正确．③y=sin|x|时偶函数，并且其图象在（0，+∞）上的图象与正弦函数的图象一致，所以函数不具有周期性．所以③错误．
④y=2sinx的周期为2π．所以④错误．
点评：本题主要考查带绝对值的三角函数的图象和性质的应用．考查三角函数的周期性和单调性，三角函数的图象是高考的重点，一定要会画图．
练习册系列答案
相关题目
-1（其中a是不为0的实数），g（x）=lnx，设F（x）=f（x）+g（x）．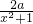
）+2m的图象与函数y=g（x2+1）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．
-1（其中a是不为0的实数），g（x）=lnx，设F（x）=f（x）+g（x）．
）+2m的图象与函数y=g（x2+1）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．