题目内容
已知数列{an}是首项为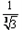
，公比为
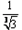的等比数列，设
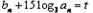，常数t∈N*.
（Ⅰ）求证：{bn}为等差数列；
（Ⅱ）设数列{cn}满足cn=anbn，是否存在正整数k，使ck,ck+1,ck+2按某种次序排列后成等比数列，若存在，求k,t的值，若不存在，说明理由.
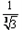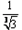，公比为的等比数列，设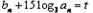，常数t∈N*.（Ⅰ）求证：{bn}为等差数列；
（Ⅱ）设数列{cn}满足cn=anbn，是否存在正整数k，使ck,ck+1,ck+2按某种次序排列后成等比数列，若存在，求k,t的值，若不存在，说明理由.
解:（Ⅰ）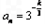
，
，
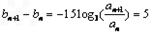∴{bn}是首项为b1=t+5,公差为5的等差数列
（Ⅱ）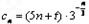
，令5n+t=x，
则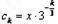
，
，
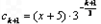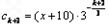
①若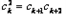
，则
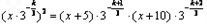
化简得：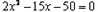
，解得x=10或
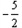（舍）
进而求得：k=1,t=5或k=2,t=0（舍）
②若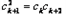
，同理可得：
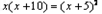，显然无解.
③若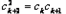
，同理可得：
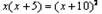，方程无整数根
综上：存在k=1,t=5适合题意.
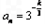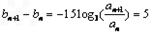，，∴{bn}是首项为b1=t+5,公差为5的等差数列
（Ⅱ）
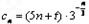，令5n+t=x，则
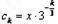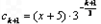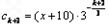
，，①若
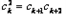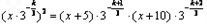
，则化简得：
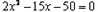，解得x=10或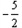（舍）进而求得：k=1,t=5或k=2,t=0（舍）
②若
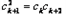，同理可得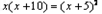：，显然无解.③若
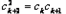，同理可得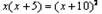：，方程无整数根综上：存在k=1,t=5适合题意.
练习册系列答案
阅读快车系列答案
相关题目