题目内容

如图，直线AA1、BB1、CC1相交于点O，AO=A1O，BO=B1O，CO=C1O，形成两个顶点相对、底面水平的三棱锥，设三棱锥高均为1，若上面三棱锥中装有高度为0.5的液体，若液体流入下面的三棱锥，则液体高度为
1-
37
2
1-
37
2
．
分析：先推导出液体部分三棱锥的体积，然后根据体积比和对应高度立方比之间的关系建立方程，即可解出液体的高度．
解答：解：液体部分的体积为三棱锥体积的
1
8
，流下去后，液体上方空出三棱锥的体积为三棱锥体积的
7
8
，
设空出三棱锥的高为x，则根据体积之比等于对应高的立方比得
x3
13
=
7
8
，
解得x=
37
2
，∴液面的高度为1-
37
2
．
故答案为：1-
37
2
．
点评：本题主要考查三棱锥的体积公式的计算，以及利用体积比和对应高的立方比之间的关系求棱锥的高，考查学生的计算能力．
练习册系列答案
相关题目
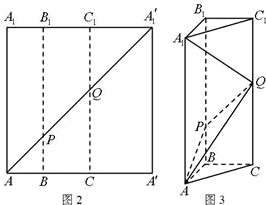精英家教网如图2所示，在边长为12的正方形AA'A'1A1中，点B，C在线段AA'上，且AB=3，BC=4，作BB1∥AA1，分别交A1A'1、AA'1于点B1、P，作CC1∥AA1，分别交A1A'1、AA'1于点C1、Q，将该正方形沿BB1、CC1折叠，使得A'A1′与AA1重合，构成如图3所示的三棱柱ABC-A1B1C1．
（1）在三棱柱ABC-A1B1C1中，求证：AB⊥平面BCC1B1．
（2）求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比．
（3）在三棱柱ABC-A1B1C1中，求直线AP与直线A1Q所成角的余弦值．
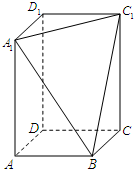精英家教网在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=4，过A1、C1、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD-A1C1D1．
（1）求几何体ABCD-A1C1D1的体积；
（2）求直线BD1与面A1BC1所成角的大小．（用反三角表示）
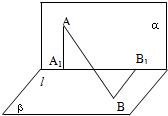精英家教网如图，α⊥β，α∩β=l，A∈α，B∈β，点A在直线l上的射影为A1，点B在l的射影为B1，已知AB=2，AA1=1，BB1=
2
，求：
（Ⅰ）直线AB分别与平面α，β所成角的大小；
（Ⅱ）二面角A1-AB-B1的大小．
（2003•北京）如图，三棱柱ABC-A1B1C1的底面是边长为3的正三角形，侧棱AA1垂直于底面ABC，AA1=
3
3
2
，D是CB延长线上一点，且BD=BC．
（1）求证：直线BC1∥平面AB1D；
（2）求二面角B1-AD-B的大小；
（3）求三棱锥C1-ABB1的体积．
附加题（必做题）
如图，在直三棱柱ABC-A1B1C1中，AC=3，BC=4，AB=5，AA1=4．
（1）设
AD
=λ
AB
，异面直线AC1与CD所成角的余弦值为
9
25
，求λ的值；
（2）若点D是AB的中点，求二面角D-CB1-B的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网