题目内容
记函数f(x)=max{p(x),q(x)},若p(x)=|x|,q(x)=-x2+2,则函数f(x)的最小值为
1
1
.分析:确定函数的解析式,可得函数的图象,从而可求函数f(x)的最小值.
解答:解:由-x2+2=x(x>0),可得x=1
∵p(x)=|x|,q(x)=-x2+2,
∴f(x)=max{p(x),q(x)}=
,图象如图所示

∴函数f(x)的最小值为1
故答案为:1
∵p(x)=|x|,q(x)=-x2+2,
∴f(x)=max{p(x),q(x)}=
|

∴函数f(x)的最小值为1
故答案为:1
点评:本题考查新定义,考查数形结合的数学思想,考查学生分析转化问题的能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
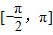 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线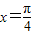 对称,当
对称,当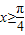 时,函数f(x)=sinx.
时,函数f(x)=sinx.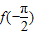 ,
,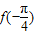 的值;
的值;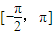 上的函数y=f(x)的图象关于直线
上的函数y=f(x)的图象关于直线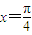 对称,当
对称,当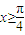 时,函数f(x)=sinx.
时,函数f(x)=sinx.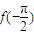 ,
,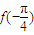 的值;
的值;